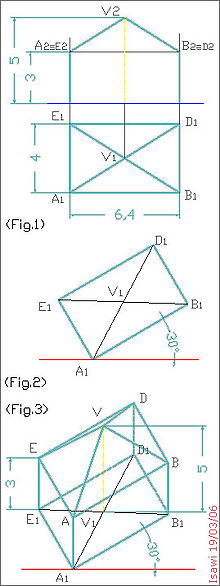
Schrägriss

Der Schrägriss ist eine abstrahierte, zeichnerisch dargestellte, zweidimensionale Abbildung einer räumlichen Gegebenheit. Schrägrissdarstellungen finden sich in technischen Zeichnungen, insbesondere jedoch in Entwurfszeichnungen der Architektur. In der darstellenden Geometrie existieren neben dem Schrägriss auch der Grundriss, zusätzlich auch Ansichten und Schnitte.

Beim Schrägriss ist die Bildebene parallel zu einer Koordinatenebene gewählt. Da alle Ebenen, die zur Bildebene parallel liegen, kongruent abgebildet werden, kann man in diesem Fall das axonometrische Bild besonders einfach zeichnen, er ist also ein Spezialfall der Axonometrie.

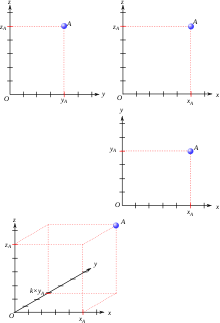
Ein Schrägriss enthält immer ein Achsenkreuz, zumeist mit der Bezeichnung: x-, y-, und z-Achse. Ebenso sind für jede Achse Verzerrungsfaktoren festgelegt.

Spezielle Schrägrisse

^[1]

Frontalriss oder auch Kavalierriss

Erläuterung des Frontalrisses bzw. des Kavalierrisses. Mit Bezug auf die Formel ist x" gleich x_A, usw.

Würfeldarstellung im Frontalriss bzw. auch Kavalierriss genannt

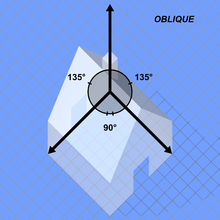
Beim Kavalieriss (englisch: cavalier projection, cavalier perspective oder high view point) ist der Winkel zwischen der z- und y-Achse immer mit 90° gewählt und der Verzerrungsfaktor der y- und z-Achse immer 1. Die Länge der dritten Achse ist zumeist kleiner 1 skaliert.^[2][3]

Diese Art des Schrägrisses ist relativ einfach freihand zu zeichnen. Oft benutzt wird dieser, wenn man erst die Ansicht gezeichnet hat, um dann die dritte Dimension hinzuzufügen.

Die Darstellungsart wurde ursprünglich für militärische Befestigungen – Erdhügelbefestigungen – verwendet, in der Art wie diese ein Reiter sehen kann. Im italienischen bedeutet «cavaliere» wörtlich Reiter. Des Kavaliers Perspektive ist also so wie die Dinge aus diesem Höhepunkt gesehen wurden. Eine andere Worterklärung ist, dass diese Darstellungsart durch den Mathematiker Bonaventura Cavalieri erstmalig beschrieben wurde.

Mathematische Formulierung

Wenn die Bildebene xz und die Fluchtrichtung die y-Achse unter einen Winkel von α ist, dann wird ein Punkt im Raum mit den Koordinaten (x, y, z) auf der Bildebene durch einen (x", y") Punkt abgebildet:

• x" = x + cos α·y;
• y" = z + sin α·y.

Die Transformationsmatrix ist

$P = \begin{pmatrix} 1 & \cos \alpha & 0 \\ 0 & \sin \alpha & 1 \end{pmatrix}$

Zum Beispiel für einen Winkel von 30°, einer Länge von 1 und einen Verzerrungsfaktor von 0,7:

• x" = x + 0,35·y;
• y" = z + 0,6062·y;

Zum Beispiel für einen Winkel von 45°, einer Länge von 1 und einen Verzerrungsfaktor von 0,5:

• x" = x + 0,3535·y;
• y" = z + 0,3535·y;

Siehe auch: Kavalierperspektive was die perspektivische Darstellung mit unverzertem Aufriss sein sollte.

Horizontalriss oder Militärriss

Erläuterung des Horizontalrisses bzw. des Militärrisses

Zeichnung im Militärriss

Konstruktive Anleitung, wie aus einem Grund- und Aufriss einfach ein Militärriss aufgebaut wird

Beim Horizontalriss oder auch Militärriss genannt, wobei der Winkel zwischen der x- und y-Achse immer mit 90° gewählt wird und der Verzerrungsfaktor der x- und y-Achse immer 1 ist.

Beim Freihandzeichnen von Gebäuden und Objekten kann man diesen Schrägriss relativ einfach aus dem Grundriss heraus aufbauen. Er ist deshalb bei Designern als Darstellungsmethode im Entwurf auch beliebt.

Einschneideriss

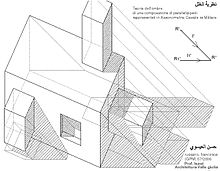
Beim Einschneideriss wird der Grundriss des Körpers um einen beliebigen Winkel gedreht und verschoben. Der Aufriss wird in seiner gewohnten Lage belassen. Mit dieser Bildern konstruiert man dann das axionometrische Bild und deshalb werden diese Risse Einschneiderisse genannt.

Siehe auch

• Walter Wunderlich: Darstellende Geometrie, 2 Bände. BI Wissenschaftsverlag 1966, 1967
  
• Hannes Rassi: Grundlagen Projektion versus Perspektive (PDF)

Weblinks

 Commons: Oblique projection – Sammlung von Bildern, Videos und Audiodateien

Einzelnachweise

1. ↑ Studienunterlage: Erläuterung der schiefen Axionimetrie FH-Campus Wien
2. ↑ Illustrator Draftsman 3 & 2 – Volume 2, Standard Practices and Theory, page 67
3. ↑ Ingrid Carlbom, Joseph Paciorek: Planar Geometric Projections and Viewing Transformations. ACM Computing Surveys, v.10 n.4, pp. 465–502, Dec. 1978