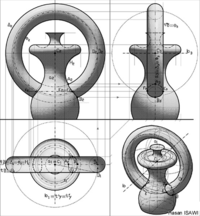
- Darstellende Geometrie
-
Eine Nachmodellierung der Tower Bridge mit Hilfe eines CAD-Programms

Darstellende Geometrie ist der Teilbereich der Geometrie, der sich mit den geometrisch-konstruktiven Verfahren von Projektionen dreidimensionaler Objekte auf eine zweidimensionale Darstellungsebene befasst. Die Anwendungsbereiche ihrer Methoden sind breit gefächert und erstrecken sich neben den heute bekanntesten Anwendungen in der Technik- und Architekturdarstellung auch auf Kunst, Malerei, und das Kartenwesen.
Inhaltsverzeichnis
Methoden
In der Architekturdarstellung sowie in der perspektivischen Malerei seit der Renaissance kommen verschiedene geometrische Projektionen der darstellenden Geometrie (siehe: Perspektive) sowie Konstruktion von Schattenwürfen (siehe: Schattenwurf) zur Anwendung. Zusätzlich geht es bei der Architekturdarstellung regelmäßig um die Ermittlung wahrer Größen aus einer projektiven Darstellung und das projektive Skizzieren nach vorgegebenen Maßen (siehe Spurdreieck).
Im Bereich des technischen Zeichnens stellt die darstellende Geometrie Methoden der dreidimensionalen Objektdarstellung (meist ohne Fluchtpunkt) als Isometrie bereit.
Für Planzeichnungen, Kartenwerke und Geländedarstellungen bietet die darstellende Geometrie die kotierten Projektionen an, bei denen räumliche Höhen als Zahlenwerte ausgewählter Punkte in die Zeichnung eingetragen werden.
Außerdem liegen die Verfahren der darstellenden Geometrie dem zimmermannsgerechten Schiften von Dachstühlen zugrunde.
Ausbildung
Darstellende Geometrie ist heute ein technisch-geometrisches Fach in berufsbildenden Schulen und ein grundlegendes Fach in der Ausbildung von Ingenieuren an einer TU oder FH.
Thema ist die Erfassung und Darstellung von räumlichen, insbesondere technischen Strukturen (geometrische Körper, Bauwerke, Darstellung des Geländes usw).
Wichtigste Hilfsmittel sind Konstruktions-Zeichnungen, Perspektive (Zentralprojektion), Axonometrie, Kotierte Projektion und zugehörige Programme der Computergrafik.
Neben dem Erlernen von Zeichentechniken sollen die räumliche Vorstellungskraft und Ausdrucksweise gefördert sowie Querverbindungen zu Mathematik, zur Technik und zur Bildenden Kunst hergestellt werden. In den letzten Jahren hat die Bedeutung des Faches zwar nicht generell, aber in der Ausbildung abgenommen, weil die computergestützte Konstruktion (CAD) andere Fertigkeiten verlangt als die zeichnerische Darstellung von Hand.[1]
Die eigentliche Denkarbeit, das Umsetzen der 2D-Darstellung (ob Papier oder Bildschirm) in ein 3D-(Denk-)Modell bleibt auch bei Benutzung von CAD dem Konstrukteur oder Entwerfer erhalten. Dagegen wird es schwieriger, räumliche Konstruktionsprobleme (z. B. Anschlussprofile bei schrägen Anschnitten) zu erkennen, wenn (und weil) man sich auf die Software verlässt.
"Darstellende Geometrie ist nicht in einem oberflächlichen Sinn Voraussetzung, ein CAD-Programm zu beherrschen. Sie zu üben, ist vielmehr eine Primärerfahrung, indem die räumliche Vorstellungskraft, das Abschätzen und Auswählen von Lösungsstrategien und die Präzision des Denkens trainiert werden." Zitat Prof. Horst Sondermann, Hochschule für Technik Stuttgart
Alternativen
Grundsätzlich können alle Probleme der darstellenden Geometrie auch mit Hilfe der Vektorrechnung gelöst werden, ohne dass dazu zeichnerische Konstruktionen erforderlich sind, sofern nicht die Darstellung als solche das eigentliche Ziel der Konstruktion ist.
Siehe auch
Weblinks
 Wikibooks: Darstellende Geometrie – Lern- und Lehrmaterialien
Wikibooks: Darstellende Geometrie – Lern- und LehrmaterialienEinzelnachweise
Wikimedia Foundation.