Verstärkerlinearisierung

Bei Verstärkern bezeichnet die Verstärkerlinearisierung eine Form der Fehlerkorrektur (engl. error correction) die nichtlinearer Verzerrungen durch Messung der Abweichung, die anschließend als Korrektursignale dienen, kompensiert. Dem Übertragungssignal beigemischt erfolgt idealerweise eine vollständige Elimination aller Verzerrungen.

Grundgedanke

Die Minimierung nichtlinearer Verzerrungen durch Gegenkopplung erfordert eine hohe Kreisverstärkung. Die zunehmende Verstärkung geht mit einer größeren Gefahr der Instabilität des Regelkreises einher und erfordert deswegen schnelle Elektronik. Die Fehlerkorrektur dagegen benötigt lediglich eine Verstärkung von eins für die Messung des Fehlersignals.

Feedforward

Feedforward

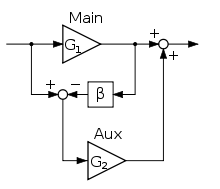
Der Signalflussplan für eine Feedforward-Fehlerkorrektur verdeutlicht das Konzept sehr gut. Die Differenz zwischen Eingangs- und Ausgangssignal vom Übertragungsglied G₁ bildet das Korrektursignal. Das Übertragungsglied G₂ agiert als Leistungsverstärker für das Korrektursignal. Dem fehlerbehafteten Signal beaufschlagt resultiert ein verzerrungsarmes Ausganganssignal.

$G_{gesamt} = \left( 1 - \beta \cdot G_1 \right) \cdot G_2 + G_1$

Das Glied β macht die Verstärkung des Eingangssignals durch G₁ rückgängig, entspricht also dessen Kehrwert. Das Korrektursignal benötigt die gleiche Verstärkung wie das Hauptsignal, daher besitzt G₂ den gleich Verstärkungsfaktur wie G₁.

$G_1 \approx \frac{1}{\beta} \ \land \ G_2 \approx G_1 \ \Rightarrow \ G_2 = \frac{1}{\beta}$

Die Voraussetzung G₂ = 1/β ermöglicht folgende Umformungen:

$G_{gesamt} = \left( 1 - \beta \cdot G_1 \right) \cdot \frac{1}{\beta} + G_1$

$G_{gesamt} = \frac{1}{\beta} - G_1 + G_1 = \frac{1}{\beta}$

Die durch die Nichtlinearität von G₁ eingebrachten Verzerrungen kürzen sich vollständig. Da keinerlei Signal-Rückführung vorhanden ist, sind Eigenschwingungen ausgeschlossen.

Error-Feedback

Active-Error-Feedback

Error-Feedback Typ A

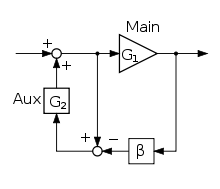
Die nebenstehende Anordnung enthält zwar eine Gegenkopplungsschleife, gesamt betrachtet handelt es sich um das Fehlerkorrektur-Prinzip. Die Regelschleife aus G₂ und β regelt solange, bis die Abweichung des Ausgangs- zum Eingangssignal gegen null geht und kompensiert damit die von G₁ eingebrachten Abweichungen.

$G_{gesamt} = \left(G_1 + G_2\right) \cdot \frac{1}{1+G_2 \cdot \beta}$

$G_2 \rightarrow \infty \land G_2 \gg G_1 \Rightarrow G_{gesamt} \approx \frac{1}{\beta}$

Damit nur Linearitätsfehler korrigiert werden gilt:

$G_1 \approx \frac {1}{\beta}$

Durch diese Struktur bleiben die von Gegenkopplung bekannten Stabiliätsprobleme erhalten. Die Verlagerung der Schleife zu G₂ bietet Vorteile, denn das Korrektursignal hat eine deutlich kleinere Amplitude und G₂ kann daher grundsätzlich anders ausgelegt werden als G₁.

Error-Feedback Typ B

Bei der zweiten Variante des Error-Feedback-Prinzips agiert nur G₁ als Leistungsverstärker. Durch entsprechendes Übertragungsverhalten von G₂ bleibt die Fehlerkorrektur auf den unteren Frequenzbereich beschränkt und daher minimiert sich die Gefahr der Schwingungsneigung. Nur ein einziges leistungsverstärktes Signal liegt am Ausgang, eine Addition von Ausgangssignalen entfällt, dies verringert die Verluste, Rückwirkung und den Ausgangswiderstand.

$G_{gesamt} = \frac{G_1 \cdot \left( 1 + G_2 \right)}{1+G_1 \cdot G_2 \cdot \beta}$

$G_2 \ \rightarrow \ \infty \ \land \ G_2 \gg G_1 \ \Rightarrow \ G_{gesamt} \approx \frac{1}{\beta}$

Damit nur Linearitätsfehler korrigiert werden gilt:

$G_1 \approx \frac {1}{\beta}$

Hawksford

Hawksford-Error-Feedback

Die ungewöhnlichste Variante machte Malcolm Hawksford für Audio-Verstärker populär. Das Verständnis zur Funktionsweise ist nicht trivial. Hier knapp zusammengefasst die mathematische Herleitung:

Parallelstruktur aus G₁, β und unterem Additionspunkt zusammenfassen:

$1-G_1 \cdot \beta$

Kreisstruktur aus G₂ und obiger Parallelstruktur auflösen:

$\frac{1}{1-G_2 \cdot \left(1- G_1 \cdot \beta \right)}$

Für das Auslagern des Ausgangssignal aus der Parallelstruktur den Knoten hinter G₁ nach vorne verschieben und anschließend mit der Kreisstruktur zusammenführen (Verschiebungsregeln):

$G_{gesamt} = G_1 \cdot G_\circ$

$G_{gesamt} = G_1 \cdot \frac{1}{1-G_2 \cdot \left(1- G_1 \cdot \beta \right)}$

$G_2 = 1 \ \Rightarrow \ G_{gesamt}= \frac{1}{\beta}$

Damit nur Linearitätsfehler korrigiert werden gilt:

$G_1 \approx \frac {1}{\beta}$

Als besonders vorteilhaft erweist sich das G₂ nur eine geringe Verstärkung von eins erfordert. Das erhöht die Stabilität der Schaltung gegenüber Eigenschwingungen.

Anmerkung: Die Gleichungen sind nur bei geringen Verzerrungen zur Stabilitätsanalyse geeignet, da G₁ nichtlinear ist und damit die LZI-Bedingungen nicht vollständig erfüllt sind.

Current Dumping

Current Dumping

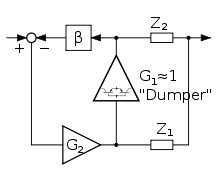
Auch Verstärker mit dem Konzept des Current Dumping gehören in die Kategorie der Fehlerkorrektur. Der Dumper ist ein Klasse-B-Gegentaktverstärker, der Verstärker G₂ dagegen ein verzerrungsarmer Klasse-A-Verstärker und liefert nur ein hundertstel der Ausgangsleistung des Dumpers.

1975 von P. J. Walter als Patent eingereicht und erteilt worden. (U.S. Patent 3,970,953, ausgelaufen)

Anwendungen

Allgemein zur Linearisierung von analogen Schaltungen. Beispiele hierfür sind:

• Verstärker_(Elektrotechnik)
• Audioverstärker
• Operationsverstärker

Weblinks

• Malcolm Hawksford
  • Distortion Correction in Audio Power Amplifiers (PDF-Datei)
  • Distortion Correction Circuits for Audio Amplifiers (PDF-Datei)
  • Towards a Generalisation of Error Correction Amplifiers (PDF-Datei; 895 kB)
• A MOSFET Power Amplifier with (Hawksfork) Error Correction, cordellaudio.com
• Feedforward Error Correction in Power Amplifiers, Vanderkooy, John; Lipshitz, Stanley P., JAES Volume 28 Issue 1/2 pp. 2-16; February 1980 (kostenpflichtig)
• paX, power amplifier eXperimental von Jan Didden
  Ausführlich beschrieben in den Elektor Ausgaben April 2008 + Mai 2008 (kostenpflichtig)

Funktechnik

• An Adaptive Feedforward Amplifier Application for 5.8 GHz, Engin Kurt und Osman Palamutcuogullari (PDF-Datei; 485 kB)
• Balanced error correction for power amplifiers, Warren Guthrie (PDF-Datei; 541 kB)