Garland-Heckbert-Algorithmus

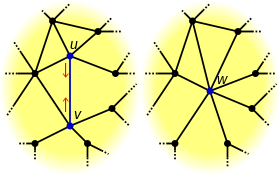
Der Garland-Heckbert-Algorithmus ist in der Computergraphik ein Verfahren, um den Detailgrad eines als Dreiecksnetz modellierten 3D-Körpers kontrolliert zu reduzieren ("simplifizieren"), ohne dabei das grundsätzliche Aussehen des Körpers zu verändern. Dies geschieht inkrementell, wobei immer eine Kante des Dreiecksnetzes gelöscht und die beiden adjazenten Knoten zu einem einzelnen Knoten zusammengefasst werden. Es wird immer diejenige Kante gelöscht, deren Entfernen die geringste optische Veränderung des Körpers bewirkt.

Geschichte

Der Algorithmus wurde 1997 in einem Paper von Michael Garland und Paul Heckbert vorgestellt^[1].

Algorithmus

Kantenkontraktion

Im einem Dreiecksnetz wird das Löschen einer Kante und Zusammenfassen der übrig gebliebenen Knoten als Kantenkontraktion oder -kollaps bezeichnet. Der Algorithmus gibt Auskunft darüber, welche Kante gelöscht werden muss, und an welcher Stelle der neu entstandene Knoten platziert wird.

Dazu wird eine Fehlerquadrik verwendet, die jedem Knoten und jeder Kante zugeordnet wird. Diese gibt Auskunft darüber, wie groß der entstehende optische Fehler wäre, wenn die entsprechende Kante kontrahiert werden würde. Gleichzeitig kann mit ihr berechnet werden, wo der neu entstehende Knoten platziert werden muss, damit genau dieser Fehler (und kein größerer) entsteht.

Pseudocode

Berechne zunächst für jeden Knoten b_i die zugehörige initale Fehlerquadrik Q_bi. Siehe dazu weiter unten.

Danach iteriere solange, bis der gewünschte Detailgrad erreicht ist:

1. Jede Kante erhält als Quadrik Q_Ej die Summe der Quadriken ihrer beiden Endpunkte.
2. Berechne anhand der Quadrik für jede Kante, an welcher Stelle der zusammengezogene Knoten erstellt werden müsste, um minimalen Fehler beim Kollabieren der Kante zu verursachen.
3. Finde unter allen Kanten diejenige, deren Fehler beim Kollabieren am kleinsten werden würde. Kollabiere diese Kante.
4. Der beim Kollaps neu entstehende Punkt bekommt als Quadrik diejenige zugewiesen, die der kollabierten Kante gehörte.

Detaillierte Beschreibung

Initiale Fehlerquadriken

Den Fehler, der beim Zusammenfassen zweier Knoten v₁ und v₂ zu einem neuen v_neu entsteht, definiert man als: Quadrat der Summe der Abstände, die v_neu zu allen Flächen hat, die durch irgendeins der Dreiecke definiert werden, welche an v₁ oder v₂ grenzen.

Um zunächst den Abstand eines Punktes v_neu zu einer Fläche F zu berechnen, kann folgende Formel verwendet werden:

$dist(v_{neu}, F) = n^T \cdot (v_{neu}-b)$

Dabei ist b ein beliebiger Punkt in der Fläche (z.B. einer der Eckpunkte des Dreiecks, das in der Fläche liegt), und n^T ist der Normalenvektor der Fläche (zum Zeilenvektor transponiert).

Bildet man nun wie vorgesehen das Quadrat dieses Abstands, erhält man:

$\begin{align} dist(v_{neu}, F)^2 &= (n^T \cdot (v_{neu}-b))^2\\ &= (n^T \cdot (v_{neu}-b)) \cdot (n^T \cdot (v_{neu}-b))\\ &= (n^Tv_{neu} - n^Tb) \cdot (n^Tv_{neu} - n^Tb)\\ &= (n^Tv_{neu})^2 - n^Tv_{neu} \cdot n^Tb - n^Tb \cdot n^Tv_{neu} + (n^Tb)^2\\ &= {v_{neu}}^Tn\cdot n^Tv_{neu} - b^Tn\cdot n^Tv_{neu} - {v_{neu}}^Tn\cdot n^Tb + b^Tn\cdot n^Tb \end{align}$

Verwendet man homogene Koordinaten, so ist diese Rechnung gleichbedeutend mit:

$dist(v_{neu}, F)^2 = ( v_{{neu}_x} v_{{neu}_y} v_{{neu}_z} 1) \cdot \begin{pmatrix} nn^T & -nn^Tb \\ -b^Tnn^T & b^Tnn^Tb\end{pmatrix} \cdot \begin{pmatrix} v_{{neu}_x} \\ v_{{neu}_y} \\ v_{{neu}_z} \\ 1 \end{pmatrix}$

Die Matrix $Q_F = \begin{pmatrix} nn^T & -nn^Tb \\ -b^Tnn^T & b^Tnn^Tb\end{pmatrix}$ wird als Fehlerquadrik der Fläche F bezeichnet.

Betrachtet man nun einen Knoten b des Dreiecksnetzes, so kann ihm als Fehlerquadrik Q_b die Summe der Quadriken seiner angrenzenden Dreiecksflächen F_i zugewiesen werden.

$Q_b = \sum_i Q_{F_i}$

Die Quadrik Q_b wird zur Initialisierung des Algorithmus für jeden Knoten des Dreiecksnetzes berechnet.

Iterationsschritt

Berechnung der zu kontrahierenden Kante

Jede Kante e_j des Dreiecksnetzes erhält als Quadrik Q_ej die Summe der Quadriken ihrer Endpunkte b₁ und b₂:

$Q_{e_j} = Q_{b_1} + Q_{b_2}$

Falls der Kante e_j vorher noch keine Quadrik zugeordnet war (nur im ersten Iterationsschritt), oder falls sich die Quadrik im Vergleich zum letzten Iterationsschritt verändert hat (weil einer der Endpunkte durch Kantenkontraktion verschoben wurde), muss nun berechnet werden:

• Welcher Punkt v_neu beim Kontrahieren von e_j einen möglichst kleinen Fehler verursachen würde
• Wie groß der verursachte Fehler wäre.

Um den optimalen Punkt v_neu zu bestimmen, muss also der Minimalwert der Fehlerfunktion gefunden werden, d.h. alle partiellen Ableitungen von $( {v_{neu}}^T \quad 1) \cdot Q_{e_j} \cdot \begin{pmatrix} v_{neu} \\ 1 \end{pmatrix}$ müssen gleich 0 sein.

Berechnet man diese Ableitungen, erhält man folgendes zu lösende Gleichungssystem:

$\begin{pmatrix} & nn^T & & -nn^Tb \\ 0 & 0 & 0 & 1\end{pmatrix} \cdot \begin{pmatrix} v_{{neu}_x} \\ v_{{neu}_y} \\ v_{{neu}_z} \\ 1 \end{pmatrix} = \begin{pmatrix}0 \\ 0 \\ 0 \\ 1 \end{pmatrix}$

Dabei können sich mehrere Fälle ergeben:

• Die Matrix $\begin{pmatrix} & nn^T & & -nn^Tb \\ 0 & 0 & 0 & 1\end{pmatrix}$ ist invertierbar: Der Punkt v_neu kann einfach durch das Gleichungssystem berechnet werden.
• Die Matrix $\begin{pmatrix} & nn^T & & -nn^Tb \\ 0 & 0 & 0 & 1\end{pmatrix}$ ist nicht invertierbar: Der optimale Wert für v_neu kann auf der Verbindungsstrecke der beiden Kantenendpunkte b₁ und b₂ gefunden werden. Man beschreibt dann v_neu als Linearkombination der beiden Endpunkte: ${v_{neu}}^*(\lambda) = (1-\lambda)\cdot b_1 + \lambda \cdot b_2$ und sucht stattdessen das Minimum von $dist(v_{neu}, F)^2 = ( ({v_{neu}}^*)^T \quad 1) \cdot Q_{e_j} \cdot \begin{pmatrix} {v_{neu}}^* \\ 1 \end{pmatrix}$ bezüglich λ. Dies geschieht durch einfache Ableitung der Funktion nach λ und setzen dieser Ableitung = 0.
• Sollte auch die zweite Methode kein Ergebnis liefern, so wird einfach der Mittelpunkt zwischen b₁ und b₂ verwendet, oder b₁ oder b₂ selbst.

Nachdem nun v_neu bekannt ist, wird der entstandene Fehler $( {v_{neu}}^T \quad 1) \cdot Q_{e_j} \cdot \begin{pmatrix} v_{neu} \\ 1 \end{pmatrix}$ berechnet. Dieser Fehler wird in eine Prioritätswarteschlange eingetragen, wobei der niedrigste Fehler das Top-Element der Warteschlange ist.

Kontrahieren der Kante

Aus der Warteschlange wird das Top-Element entfernt. Dieses Element entspricht derjenigen Kante, deren Kontraktion den geringsten Fehler verursacht. Die Kante wird nun kontrahiert, und dem dabei neu entstehenden Punkt v_neu wird die Fehlerquadrik der dabei zerstörten Kante zugewiesen. Dies bewirkt, dass der Fehler in den folgenden Iterationsschritten nicht nur von dem jeweils aktuellen Dreiecksnetz abhängt, sondern auch die vorherigen Veränderungen mit einbezogen werden.

Referenzen

1. ↑ M. Garland and P. Heckbert. Surface Simplification Using Quadric Error Metrics. In Proceedings of SIGGRAPH 97. [1]