Hebungsbaum

Ein Hebungsbaum ist ein Hilfsmittel um das Verhalten eines Polynoms $f(X)\in Z[X]$, genauer das Verhalten der Nullstellen modulo p^k des Polynoms, zu verstehen. Anhand eines Hebungsbaumes kann man p-adische Zahlen leichter untersuchen und damit auf das Verhalten des Polynoms schließen.

Bezeichnung

Sei $f(X)\in Z[X]$ ein rational irreduzibles Polynom. Sei p prim. Sei $k\geq 1$ die Ebene des Hebungsbaumes.

Sei $a\in Z$. Ist $f(a)\equiv 0\mod p^k$, so sagen wir, a ist eine Nullstelle von f(X) in Z / p^k oder modulo p^k.

Sei $a\in Z$ eine Nullstelle von f(X) modulo p^k. Sei $l\geq1$ . Ist $b\in Z$ eine Nullstelle von f(X) modulo p^{k + l} und ist $b \equiv a \mod p^k$ , dann sagen wir, dass b eine Nullstelle modulo p^{k + l} ist, die die Nullstelle a modulo p^k hebt.

Beschreibung

In einem Hebungsbaum werden alle Nullstellen eines Polynoms in Z / p^k eingetragen, wobei $k\in \Z$ die jeweilige Ebene des Hebungsbaumes ist.

Die erste Ebene des Baumes befindet sich ganz unten. Mit wachsendem k wächst der Baum von unten nach oben und es werden alle Nullstellen in der jeweiligen Ebene eingetragen.

In der untersten und damit ersten Ebene (k = 1) werden alle Nullstellen des Polynoms in Z / p eingetragen. Die Nullstellen nehmen Werte in dem Intervall [0,p − 1] an.

In der darüberliegenden zweiten Ebene (k = 2) werden alle Nullstellen des Polynoms in Z / p² eingetragen. Die Nullstellen des Polynoms nehmen Werte in dem Intervall [0,p² − 1] an. Reduziert eine solche Nullstelle in der zweiten Ebene zu einer Nullstelle in der darunterliegenden ersten Ebene in Z / p, so werden diese beiden Nullstellen mit einer Linie verbunden.

In der nächsthöhergelegenen Ebene (k = 3) werden alle Nullstellen des Polynoms in Z / p³ eingetragen. Die Nullstellen des Polynoms nehmen Werte in dem Intervall [0,p³ − 1] an. Auch hier gilt: Reduziert eine Nullstelle in der dritten Ebene zu einer Nullstelle in der darunterliegenden zweiten Ebene in Z / p², so werden diese Nullstellen mit einer Linie verbunden.

Dies gilt für alle folgenden Ebenen $k\in \Z$.

Beispiel

Sei das Polynom

f(x) = x⁴ − 3x³ − 3x² + x − 1

gegeben. Sei p = 5 prim.

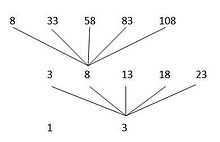
Wir erhalten folgenden Hebungsbaum:

Beispiel zu dem Polynom f(x) = x⁴ − 3x³ − 3x² + x − 1

In der ersten Ebene (k = 1) befinden sich die Nullstellen 1 und 3 in dem Intervall [0,4]. In der zweiten Ebene (k = 2) sind die Nullstellen 3, 8, 13, 18 und 23 in dem Intervall [0,24] vorhanden. In der darauffolgenden dritten Ebene (k = 3) sehen wir die Nullstellen 8, 33, 58, 83 und 108 in dem Intervall [0,124]. Für dieses Polynom gilt, dass alle Nullstellen in der zweiten Ebene zu der Nullstelle a = 3 in der ersten Ebene reduziert werden. Sie werden mit jeweils einer Linie verbunden. Man sagt kurz: Die Nullstelle a = 3 aus der ersten Ebene wird in die zweite Ebene gehoben.

Analog für die dritte Ebene.

Quellen

• Helmut Koch: Zahlentheorie - Algebraische Zahlen und Funktionen. Vieweg, 1997
• http://www.iaz.uni-stuttgart.de/LstZahltheo/Kuenzer/compprak/copra.pdf