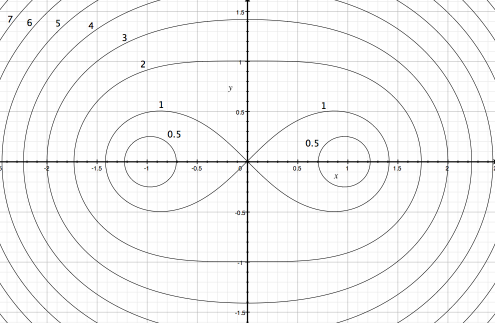
- Cassini-Kurve
-
Die Cassinische Kurve (benannt nach Giovanni Domenico Cassini) ist der Ort aller Punkte in der Ebene, für die das Produkt ihrer Abstände von zwei gegebenen Punkten (c,0) und ( − c,0) gleich a2 ist. Ein Spezialfall der Cassinischen Kurve ist die Lemniskate.
Inhaltsverzeichnis
Gleichungen
Die Kurve lässt sich in kartesischen Koordinaten durch die Gleichung
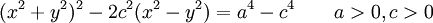
beschreiben. In Polarkoordinaten lautet die Gleichung
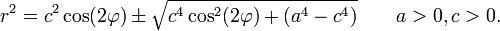
Form der Kurve
Die Form der Cassinischen Kurve lässt sich in fünf Fälle unterscheiden:
- 1. Fall
- Für
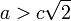 ist die Kurve ein ellipsenförmiges Oval. Ihre Schnittpunkte mit der x-Achse liegen in diesem Fall bei
ist die Kurve ein ellipsenförmiges Oval. Ihre Schnittpunkte mit der x-Achse liegen in diesem Fall bei 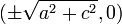 , die Schnittpunkte mit der y-Achse bei
, die Schnittpunkte mit der y-Achse bei  .
.
- 2. Fall
- Für
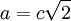 ergibt sie wieder ein ellipsenförmiges Oval. Die Schnittpunkte mit der x-Achse liegen nun bei
ergibt sie wieder ein ellipsenförmiges Oval. Die Schnittpunkte mit der x-Achse liegen nun bei 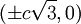 . An den Schnittpunkten mit der y-Achse bei
. An den Schnittpunkten mit der y-Achse bei 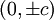 ist die Krümmung der Kurve gleich 0.
ist die Krümmung der Kurve gleich 0.
- 3. Fall
- Für
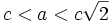 ergibt sich ein eingedrücktes Oval mit den gleichen Achsenabschnitten wie im Fall
ergibt sich ein eingedrücktes Oval mit den gleichen Achsenabschnitten wie im Fall 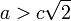 . Neben den beiden y-Achsenabschnitten sind die weiteren Extrema der Kurve an den Punkten
. Neben den beiden y-Achsenabschnitten sind die weiteren Extrema der Kurve an den Punkten 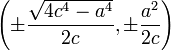 . Die vier Wendepunkte liegen bei
. Die vier Wendepunkte liegen bei 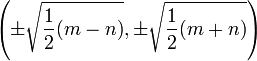 mit
mit 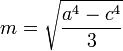 und
und 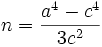 .
.
- 4. Fall
- Für a = c ergibt sich die Lemniskate.
- 5. Fall
- Für a < c ergeben sich zwei Ovale um die Punkte (c,0) und ( − c,0). Die Schnittpunkte mit der x-Achse liegen bei
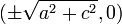 bzw.
bzw. 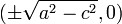 . Die Extrema sind an den Punkten
. Die Extrema sind an den Punkten 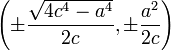 .
.
Weblink
Literatur
- Bronstein et al.: Taschenbuch der Mathematik. Verlag Harri Deutsch, Frankfurt am Main 2005, 3-8171-2006-0
Wikimedia Foundation.