Lemniskate

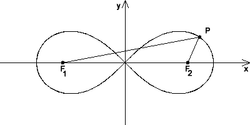Lemniskate mit durch die definierenden Punkte F₁ und F₂ gelegter Abszisse

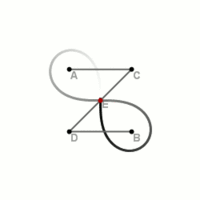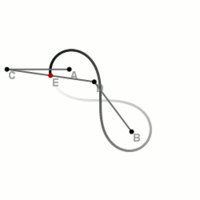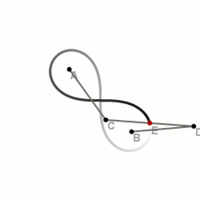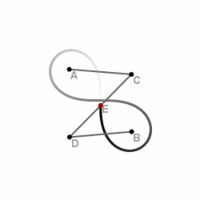Konstruktion einer Lemniskate durch einen Lemniskatenlenker

Die Lemniskate (von Latein lemniscus ‚Schleife‘) ist allgemein eine schleifenförmige geometrische Kurve. Im Speziellen ist sie das Symbol für Unendlichkeit von der Form einer liegenden Acht: $\infty$. Unicode: U+221E (∞).

Lemniskate von Bernoulli

Die Lemniskate von Bernoulli, benannt nach dem schweizerischen Mathematiker Jakob Bernoulli, ist eine ebene Kurve mit der Form einer liegenden Acht. Sie ist eine algebraische Kurve vierter Ordnung und Spezialfall einer Cassinischen Kurve.

Definition

Die Lemniskate von Bernoulli wird durch folgende geometrische Eigenschaft definiert:

Gegeben seien eine positive reelle Zahl a und zwei Punkte F₁ und F₂ im Abstand von 2a voneinander. Die Lemniskate mit den Parametern (a,F₁,F₂) ist dann der geometrische Ort aller Punkte P, für die gilt

$\overline{F_1 P} \cdot \overline{F_2 P} = a^2$.

Gleichungen der Lemniskate von Bernoulli

Es sei der Einfachheit halber vorausgesetzt, dass die Punkte F₁ und F₂ auf der Abszisse liegen und die Mitte zwischen ihnen gerade der Ursprung ist.

• Gleichung in Cartesischen Koordinaten:

$\left(x^2 + y^2 \right)^2 - 2 a^2 \left(x^2 - y^2 \right) \, = \, 0$

• Gleichung in Polarkoordinaten:

$r = a \sqrt{2 \cos(2\varphi)}$

• Parametergleichung:

$x = \frac{a\sqrt{2}\cos(t)}{\sin(t)^2 + 1}; \qquad y = \frac{a\sqrt{2}\cos(t)\sin(t)}{\sin(t)^2 + 1}$

Der Parameter a ist der Abstand zwischen Koordinatenursprung und den beiden definierenden Punkten F1 und F2. Die Strecke von F1 zu F2 hat also die Länge 2a.

Eigenschaften

Die Lemniskate von Bernoulli hat die folgenden Eigenschaften:

• Sie ist achsensymmetrisch zur Verbindungsgeraden von F₁ und F₂.
• Sie ist achsensymmetrisch zur Mittelsenkrechten zwischen F₁ und F₂
• Sie ist punktsymmetrisch zum Mittenpunkt zwischen F₁ und F₂
• Auf der Verbindungsgeraden von F₁ und F₂ liegen von allen Punkten der Lemniskate nur der Mittenpunkt zwischen F₁ und F₂ und die diesem fernsten beiden Kurvenpunkte im Abstand $(a \sqrt{2}|0)$.
• Der Mittenpunkt zwischen F₁ und F₂ ist ein Doppelpunkt der Kurve, er wird also zweimal durchlaufen. Die beiden Tangenten in ihm schneiden die Verbindungsgerade von F₁ und F₂ in einem Winkel von 45°.

Fläche

• Die beiden von der Lemniskate eingeschlossenen Teilflächen haben jeweils den Flächeninhalt a².

Bogenlänge

Die Gesamtbogenlänge der Lemniskate ist linear in a und kann unter Verwendung des von Giulio Carlo Fagnano dei Toschi um 1750 untersuchten elliptischen Integral

$F(x) \overset{\underset{\mathrm{def}}{}}{=} \int_0^x\frac{dt}{\sqrt{1-t^4}}$

explizit angegeben werden als

$a\sqrt{2}\int_{-1}^1\frac{dt}{\sqrt{1-t^4}} = 2a\sqrt{2}F(1)$

oder, mit Verwendung der im Jahr 1798 von Carl Friedrich Gauß eingeführten lemniskatischen Konstante

$\varpi \overset{\underset{\mathrm{def}}{}}{=} 2\int_0^1\frac{dt}{\sqrt{1-t^4}}$ = 2,62205755429211981… ,

als

$a\sqrt{2}\varpi$,

was ungefähr 3,708 a ist.

Vorkommen

Die Lemniskate tritt als Bewegungskurve im Wattschen Parallelogramm bzw. Wattgestänge auf sowie bei der Lemniskatenanlenkung eines Eisenbahnradsatzes.

Andere Lemniskaten

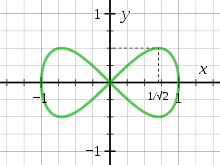Die Lemniskate von Gerono ist eine weitere Lemniskate. Sie ist eine spezielle Lissajous-Figur.

• die Lemniskate von Booth (Andrew D. Booth)
• die Lemniskate von Gerono (Camille-Christophe Gerono)

Symbolik in der Freimaurerei

Die Freimaurerei kennt die Lemniskate als Symbol für die weltweite Bruderkette. Die Schleife wird mit der Zwölfknotenschnur oder auch beim Vereinigungsband (Liebesseil) gebildet. Man findet sie beispielsweise auf den sogenannten Arbeitsteppichen der kontinentaleuropäischen Johannislogen. (Siehe auch: Acht, Endacht).

Siehe auch

• Lemniskatische Konstante
• Lemniskatenlenker
• Lemniskatischer Sinus

Literatur

• Max Koecher, Aloys Krieg: Elliptische Funktionen und Modulformen, 2. Aufl., Springer-Verlag, Berlin 2007, ISBN 978-3-540-49324-2

Weblinks

• Eric W. Weisstein: Lemniscate. In: MathWorld. (englisch)