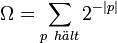Chaitins Konstante

Die chaitinsche Konstante gibt die Wahrscheinlichkeit an, mit der eine universelle Turingmaschine für eine beliebige Eingabe anhält.

Ω ist ein Beispiel für eine nicht berechenbare Zahl. Sie ist nach Gregory Chaitin definiert als

$\Omega=\sum_{p\ h\ddot a lt}2^{-\left|p\right|}$

wobei die Summe über alle haltenden Programme p gemeint ist (alle Programme, die nach endlicher Laufzeit halten) und | p | die Länge des Programms in Bit bezeichnet. Das bedeutet also, dass jedes haltende Programm der Länge m Bit das m-te Bit der Binärdarstellung von Ω um 1 erhöht.

Bemerkung: Da es gewisse Freiheiten gibt, universelle Turingmaschinen zu definieren, hängt der genaue Wert der Konstante von der gewählten Maschinendefinition ab.

Durch Kenntnis der ersten n Bit der Konstante lässt sich das Halteproblem für bis zu n Bit lange Programme entscheiden, sodass sich durch genaue Kenntnis der ersten paar tausend Bit der Konstante viele interessante Probleme der Mathematik lösen ließen.

Da das Halteproblem aber nicht lösbar ist, kann Ω nicht berechenbar sein und ist also eine transzendente reelle Zahl.

Eine Forschergruppe um Christian Calude von der Universität Auckland bestimmte im Jahr 2002 durch Überprüfen aller Turingprogramme von bis zu 64 Bit Länge die ersten 64 Bit der Zahl. Hierbei ist allerdings anzumerken, dass sich aufgrund des Aufbaus der Zahl eine Änderung an irgendeiner Dezimalstelle der Zahl auf alle vorigen auswirken kann, weshalb es unmöglich ist, die „tatsächlichen“ ersten Ziffern der Zahl zu bestimmen.

Literatur

• Jörg Resag: Die Grenzen der Berechenbarkeit, Online-Veröffentlichung, www.joerg-resag.de, 2008, Kapitel 3.4

Weblinks

• Eric W. Weisstein: Chaitinsche Konstante auf MathWorld (englisch)
• Cristian S. Calude’s Website (die ersten 64 Bit einer chaitinschen Konstante)