LCF-Notation

Der Foster-Graph: Bezeichnet man den obersten Knoten mit v₀, dann ist

90, [17,-9,37,-37,9,-17], 15

eine zugehörige LCF-Notation.

In der Kombinatorik als Teilgebiet der diskreten Mathematik ist die Lederberg-Coxeter-Fruchte-Notation (kurz LCF) eine kompakte Darstellung endlicher kubischer hamiltonscher Graphen. Die Notation geht auf Joshua Lederberg^[1] zurück und wurde von H. S. M. Coxeter und Robert Frucht erweitert.^[2] Viele Programme zur Manipulation von Graphen unterstützen LCF-Eingaben.^[3]

Syntax

Jeder LCF-Code hat folgende Form:

$n, \left[s_0,s_1,\dots s_k \right] , p$

Dabei ist n = | V | die Zahl der Knoten, die s_i sind Elemente aus einem vollständigen System kleinster Reste modulo n ohne die Null (mit anderen Worten ganze Zahlen aus $\left( \left[-\lfloor \frac{|V|}{2}\rfloor,\lfloor\frac{|V|}{2}\rfloor \right]\setminus \{0\} \right)\subset \mathbb{Z}$) und $p\in\mathbb{N}$ ist ein Iterationsparameter, so dass $k\cdot p=n$. In gedruckten Publikationen schreibt man auch $\left[s_0,s_1\dots s_k\right]^p$.

Interpretation

Zunächst wird ein Kreis der Länge n mit Knoten $\{v_0, v_1\dots v_n\}$ erstellt. Beginnend bei i = 0 bis $i=k\cdot p$ werden die Sehnenkanten $\left(v_i,v_{(s_{i~\%~k})~\%~n}\right)$ zum Kreis hinzugefügt, falls sie noch nicht existieren. Dabei bezeichnet $\%$ den Modulooperator.^[4]

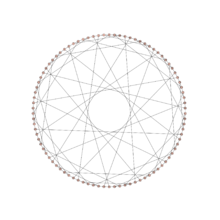
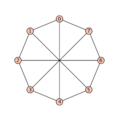
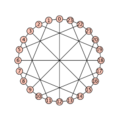
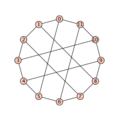
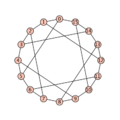
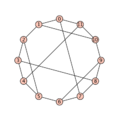
Ein Verfahren, um umgekehrt zu einem Graphen einen LCF-Code zu berechnen, lässt sich dann leicht konstruieren.^[5] LCF-Notationen zu einem Graphen sind im Allgemeinen nicht eindeutig bestimmt. Sie hängen von der Wahl des Startknotens v₀ und von der Wahl des Hamiltonkreises ab (dort hat man stets wenigstens die Wahl einer Orientierung). Umgekehrt kann es aber zu jeder LCF-Notation nur einen, bis auf Isomorphie, eindeutigen Graphen geben. Stellt man LCF-Code zusammen mit einem Plot dar, ist es Konvention, die Knoten, wenn sie nicht nummeriert sind, entlang des gewählten Hamiltonkreises „kreisförmig“ (genauer polygonal) zu setzen, wobei der Knoten v₀ „ganz oben“ steht.

• Einige Plots mit LCF-Codes
• 

  Der Wagner-Graph:

  8, [-4], 8
  

• 

  Der McGee-Graph:

  24, [12,7,-7], 8
  

• 

  Der Franklin-Graph:

  12, [5,-5], 6
  

• 

  Der Möbius-Cantor-Graph:

  16, [5,-5], 8
  

• 

  Der Franklin-Graph: (alternative Darstellung)

  12, [-5,-3,3,5], 3
  

Weblinks

• Weisstein, Eric W., LCF Notation bei MathWorld.

Einzelnachweise

1. ↑ Lederberg, J. "DENDRAL-64: A System for Computer Construction, Enumeration and Notation of Organic Molecules as Tree Structures and Cyclic Graphs. Part II. Topology of Cyclic Graphs." Interim Report to the National Aeronautics and Space Administration. Grant NsG 81-60. December 15, 1965. [1].
2. ↑ Coxeter, H. S. M.; Frucht, R.; and Powers, D. L. Zero-Symmetric Graphs: Trivalent Graphical Regular Representations of Groups. New York: Academic Press, 1981.
3. ↑ Beispielsweise Maple, NetworkX, R, sage und wahrscheinlich weitere.
4. ↑ Siehe Dokumentation der entsprechenden Klasse von Sage.
5. ↑ Ansonsten kann man es hier nachlesen: R. Frucht: A Canonical Representation of Trivalent hamiltonian Graphs Journal of Graph Theory 1, 46 - 60 (1976)