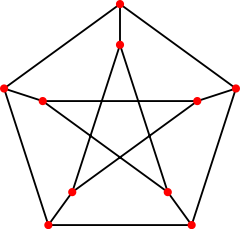
Petersen-Graph

Petersen-Graph

Benannt nach	Julius Peter Christian Petersen
Größe	10 Knoten, 15 Kanten
Eigenschaften	snark, kubisch.
Chromatische Zahl	3
Chromatischer Index	4
Knotenzusammenhang	3
Cliquenzahl	2
Schnittzahl	2
Chromatisches Polynom	t(t − 1)(t − 2)(t7 − 12t6 + 67t5 − 230t4 + 529t3 − 814t2 + 775t − 352)
Charakteristisches Polynom	(t − 1)5(t + 2)4(t − 3)
LCF-Notation

Der Petersen-Graph (benannt nach dem dänischen Mathematiker Julius Petersen) ist ein 3-regulärer (also kubischer) Graph mit 10 Knoten. Das bedeutet, dass jeder der Knoten drei Nachbarn hat, die Valenzenfolge ist also (3,3,3,3,3,3,3,3,3,3). Der Petersen-Graph ist in der Graphentheorie ein oft verwendetes Beispiel und Gegenbeispiel.

Eigenschaften des Petersen-Graphen:

• Kubisch bzw. 3-regulär (per Definition)
• Nicht planar
• Zusammenhängend
• Symmetrisch
• Die Länge des kürzesten Kreises ist 5
• Enthält keinen Hamilton-Kreis
• Kleinster hypohamiltonscher Graph
• Chromatische Zahl (Graphentheorie) 3
• Chromatischer Index (Graphentheorie) 4

Der Petersen-Graph gehört zu einer Gruppe von zusammenhängenden, brückenlosen und nicht planaren Graphen, die als „Snark“ bezeichnet werden.

Siehe auch: Typen von Graphen in der Graphentheorie

Weblinks

• Eric W. Weisstein. "Petersen Graph." From MathWorld--A Wolfram Web Resource. (englisch)
•  Commons: Petersen-Graph – Sammlung von Bildern, Videos und Audiodateien