Markoff-Zahl

Die ersten Einträge im Baum der Markoff-Zahlen

Eine Markoff-Zahl (nach Andrei Andrejewitsch Markow) ist eine natürliche Zahl x, y oder z, die als Lösung der diophantischen Markoff-Gleichung

$x^2 + y^2 + z^2 = 3xyz\,$

vorkommt. Die ersten Markoff-Zahlen sind

1, 2, 5, 13, 29, 34, 89, 169, 194, 233, 433, 610, 985, 1325,…

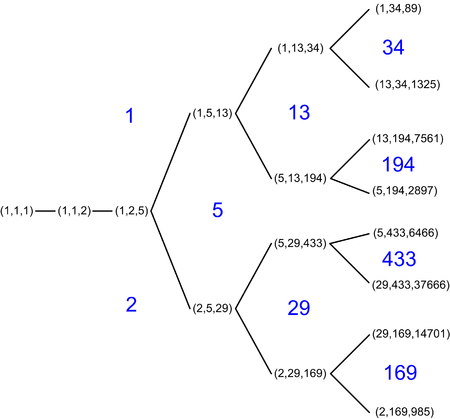
Sie sind Teile der Lösungen der Markoff-Gleichung, von denen die ersten (1, 1, 1), (1, 1, 2), (1, 2, 5), (1, 5, 13), (2, 5, 29) lauten. Die Lösungen werden auch als Markoff-Tripel bezeichnet.^[1][2]

Markoff-Zahlen kommen in der Theorie der Quadratischen Formen und der diophantischen Approximationen vor: Ist m eine Markoff-Zahl, so ist $m/\sqrt{9m^2-4}$ sowohl ein Element des sogenannten Markoff-Spektrums (quadratische Formen) als auch des Lagrange-Spektrums (diophantische Approximationen).

Eigenschaften

Es gibt unendlich viele Markoff-Zahlen und -Tripel. Da die Markoff-Gleichung symmetrisch in den Variablen ist, kann man die Lösungstripel (x, y, z) der Größe geordnet mit x ≤ y ≤ z angeben. Mit Ausnahme der beiden kleinsten Tripel (1,1,1) und (1,1,2) bestehen die Lösungstripel (x, y, z) aus drei verschiedenen Zahlen. Eine seit langer Zeit untersuchte – aber noch unbewiesene – Vermutung besagt, dass das größte Element z eines Tripels schon das Markoff-Tripel (x, y, z) bestimmt.^[3]

Die Markoff-Zahlen können wie rechts abgebildet in einem Baum angeordnet werden. Die zur Region 1 benachbarten Markoff-Zahlen sind die Fibonacci-Zahlen f_i mit ungeradem i. Die zur Region 2 benachbarten Markoff-Zahlen sind die sogenannten Pell-Zahlen p_i mit ungeradem i.^[4]

Ist eine Markoff-Zahl m ungerade, so erfüllt sie die Kongruenz m ≡ 1 mod 4 und wenn sie gerade ist, dann gilt m ≡ 2 mod 32.^[5] Die drei Markoff-Zahlen eines Tripels sind stets paarweise teilerfremd.

Die Erzeugung neuer Markoff-Tripel aus bekannten

Man kann aus einer Lösung (x, y, z) der Markoff-Gleichung mittels (x, y, z) → (x, y, 3xy - z) weitere Lösungen erzeugen.^[6] Dabei ist es nicht nötig, dass die Lösung, mit der man beginnt, der Größe nach geordnet ist. Die unterschiedlichen Anordnungen von x, y und z können unterschiedliche Tripel (x, y, 3xy - z) erzeugen.

Nimmt man zum Beispiel (1, 5, 13), dann bekommt man die drei benachbarten Tripel (5, 13, 194), (1, 13, 34) und (1, 2, 5) im Markoff-Baum, wenn man x gleich 1, 5 oder 13 setzt. Wendet man (x, y, z) → (x, y, 3xy - z) zweimal an, ohne die Einträge im Tripel umzusortieren, so bekommt man wieder das Ausgangstripel.

Fehler der Approximation für die ersten 1000 Markoff-Zahlen

Beginnt man mit (1, 1, 2) und vertauscht fortwährend y und z vor jeder Transformation, so erzeugt man damit die oben erwähnten Markoff-Tripel, die Fibonacci-Zahlen enthalten. Mit dem gleichen Starttripel aber mit Vertauschen von x und z erzeugt man die Pell-Lösungen.

Wie groß ist die n-te Markoff-Zahl?

Im Jahr 1982 bewies Don Zagier eine asymptotische Formel für die Anzahl der Markoff-Tripel unterhalb einer Schranke und vermutete, dass die n-te Markoff-Zahl asymptotisch gegeben ist durch

$m_n = \tfrac13 e^{C\sqrt{n}+o(1)}$ mit C = 2.3523418721…

(hier wird die O-Notation von E. Landau verwendet).^[7][8] Der Fehler (log(3m_n) / C)² − n ist in der nebenstehenden Abbildung illustriert. Die 1000. Markoff-Zahl ist ca. 6· 10³¹.^[9]

Einzelnachweise

1. ↑ Siehe auch den Abschnitt „Die Markoff-Zahlen“ in Paulo Ribenboims Buch „Meine Zahlen, meine Freunde“: Google Books
2. ↑ Die Markoff-Zahlen sind die Folge A002559 in Neil Sloanes Online Encyclopedia of Integer Sequences.
3. ↑ Der Lösungsansatz von Norbert Riedel aus dem Jahr 2007 (Markoff Equation and Nilpotent Matrices, arXiv) wird diskutiert in dem langen Artikel von Serge Perrine: De Frobenius à Riedel: analyse des solutions de l'équation de Markoff, Archive-Ouvertes.
4. ↑ Diese genügen, mit den Startwerten p₀ = 0 und p₁ = 1, der Rekursion p_i = 2p_{i − 1} + p_{i − 2}. Die Pell-Zahlen mit ungeradem i haben die Eigenschaft, dass $2p_i^2 - 1$ eine Quadratzahl ist (sie sind Lösungen y der Pellschen Gleichung $x^2-2y^2=-1\,$).
5. ↑ Ying Zhang: Congruence and Uniqueness of Certain Markov Numbers, Acta Arithmetica 128 3, 2007, 295–301
6. ↑ Es gilt nämlich $x^2 + y^2 + (3xy-z)^2 = x^2 + y^2 + z^2 + 9x^2y^2 - 6xyz = 9x^2y^2 - 3xyz = 3(3xy-z)xy\,$.
7. ↑ Don B. Zagier: On the Number of Markoff Numbers Below a Given Bound, Mathematics of Computation 160, 1982, 709–723, online
8. ↑ Siehe den Vortrag von M. Waldschmidt.
9. ↑ Liste der ersten tausend Markoff-Zahlen von T. D. Noe auf Sloanes Online Encyclopedia of Integer Sequences-Seite der Folge A002559.

Literatur

• Thomas Cusick, Mari Flahive: The Markoff and Lagrange spectra, Math. Surveys and Monographs 30, AMS, Providence, 1989
• Serge Perrine: La théorie de Markoff et ses développements, Tessier & Ashpool, 2002, arXiv
• Caroline Series: The Geometry of Markoff Numbers, The Mathematical Intelligencer 7 (3), 1985, 20–29.
• Eric W. Weisstein: Markov number. In: MathWorld. (englisch)