Radiale Basisfunktion

Eine radiale Basisfunktion (RBF) ist eine reelle Funktion, deren Wert nur vom Abstand zum Ursprung abhängt, so dass $\varphi(\mathbf{x}) = \varphi(\|\mathbf{x}\|)$. Der Name kommt daher, dass die Funktion nach dieser Definition radialsymmetrisch ist und ferner diese Funktionen als Basisfunktionen einer Approximation verwendet werden. Allgemeiner kann man den Abstand zu einem Punkt c betrachten, der Zentrum genannt wird, so dass $\varphi(\mathbf{x}, \mathbf{c}) = \varphi(\|\mathbf{x}-\mathbf{c}\|)$.

Eigenschaften

Jede Funktion $\varphi(x)$ für die $\varphi(\mathbf{x}) = \varphi(\|\mathbf{x}\|)$ gilt ist eine RBF. Als Norm $\|\cdot\|$ wird gewöhnlich die euklidische Norm gewählt, je nach Problem sind auch andere Normen möglich. Nimmt man beispielsweise die von der Lukaszyk-Karmowski Metrik induzierte Norm, so ist es bei manchen RBFs möglich, Probleme mit schlecht konditionierten Matrizen zu umgehen, die zur Berechnung der Koeffizienten, die bei Approximation durch RBFs auftreten, erforderlich sind.

Approximation durch RBFs

Typischerweise werden Linearkombinationen von radialen Basisfunktionen zur Approximation von Funktionen genutzt: $\textstyle y(\mathbf{x}) \approx \sum_{i=1}^N \lambda_i \varphi(\|\mathbf{x} - \mathbf{c}_i\|)$.

Hierbei wird die zu approximierende Funktion y(x) durch eine Summe von N radialen Basisfunktionen angenähert, die verschiedene Zentren c_i haben und durch die Koeffizienten λ_i gewichtet sind.

Approximationsmethoden dieser Art werden zur Modellierung nichtlinearer Systeme (mit ausreichend einfachen chaotischem Verhalten) und zur 3D Rekonstruktion in der Computergrafik (beispielsweise hierarchische RBFs) eingesetzt.

Weitere Anwendungsbereiche von RBFs sind das Lösen von partiellen Differentialgleichungen (z.B. mittels gitterfreier Kollokation) oder Transformationen bei der Bildregistrierung.

Beispiele

• 

  TPS mit $\epsilon = 1.2$

• 

  IMQ mit $\epsilon = 1.2$

• 

  gaußsche RBF mit $\epsilon = 1.2$

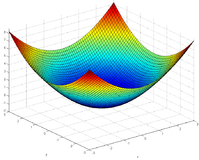
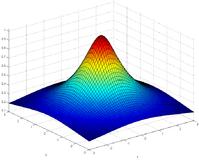
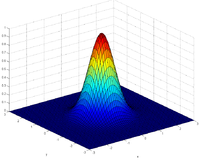
Stückweise polynomielle RBF (Rn)	| r | n, für n ungerade
Thin Plate Spline (TPSn)	| r | nln | r | , für n gerade
Multiquadric RBF (MQ)	$\sqrt{1+(\epsilon r)^2}$
Inverse multiquadric RBF (IMQ)	$\frac{1}{\sqrt{1+(\epsilon r)^2}}$
Inverse quadric RBF (IQ)	$\frac{1}{1+(\epsilon r)^2}$
gaußsche RBF (GS)	$e^{-(\epsilon r)^2}$

Neuronale Netze

Insofern als Künstliche neuronale Netze eine zur Approximation geeignete Verfahrensart sind, besonders bei hochdimensionalen Problemen, stellen RBF ein spezielles Modell für solche Netze dar.

Literatur

• Martin D. Buhmann: Radial Basis Functions: Theory and Implementations Cambridge University Press 2003
• E. Larsson, B. Fornberg: A Numerical Study of some Radial Basis Function based Solution Methods for Elliptic PDEs, Computers & Mathematics with Applications Volume 46, 2003
• H. Wendland: Scattered Data Approximation, Cambridge University Press, 2005