- Satz von Kirchhoff-Trent
-
Der Satz von Kirchhoff-Trent, auch Matrix-Gerüst-Satz genannt, dient zur Berechnung der Anzahl der Gerüste in einem Graphen.
Aussage
Die Determinante der Matrix Ai ist gleich der Anzahl der Gerüste des Graphen. Die Matrix Ai entsteht aus der Admittanzmatrix des Graphen, aus der die i-te Zeile und die i-te Spalte gestrichen werden. Die Admittanzmatrix ist die Differenz zwischen der Valenzmatrix und der Adjazenzmatrix des Graphen.
Beispiel
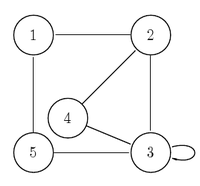
Gegeben sei der Graph auf der Abbildung rechts. Die Adjazenzmatrix ist
 .
.In der ersten Zeile steht in der zweiten und fünften Spalte eine 1, da der Knoten 1 mit den Knoten 2 und 5 adjazent, also verbunden ist.
Die Valenzmatrix gibt die Anzahl der Nachbarknoten eines Knotens an. Daher sieht die Valenzmatrix folgendermaßen aus.

Da Knoten 2 mit drei anderen Knoten verbunden ist, steht in der zweiten Zeile in der zweiten Spalte der Matrix eine 3.
Berechnung der Admittanzmatrix:

Streicht man die dritte Zeile und Spalte erhält man die Matrix
 . Auch durch Streichen anderer Zeilen und Spalten erhält man die korrekte Lösung.
. Auch durch Streichen anderer Zeilen und Spalten erhält man die korrekte Lösung.Abschließend muss die Determinante der Matrix A3 berechnet werden. Als Lösung erhält man 11.
Wikimedia Foundation.