Verschlingungszahl

In der Mathematik ist die Verschlingungszahl eine Invariante, die die Verschlingung zweier sich nicht durchdringender, geschlossener Kurven im dreidimensionalen Raum beschreibt. Die Verschlingungszahl ist immer eine ganze Zahl und kann je nach Orientierung (Durchlaufrichtung) der Kurven positiv oder negativ sein. Rein intuitiv stellt die Verschlingungszahl die Anzahl der Windungen der Kurven umeinander dar.

Berechnung der Verschlingungszahl

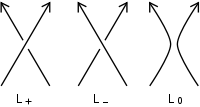
Wir betrachten zwei geschlossene Kurven J und K, für die jeweils eine Orientierung (Durchlaufrichtung) gegeben ist. Die Verschlingungszahl $lk(J,K)\,$ von J und K ist durch die Anzahl der positiven und negativen Kreuzungen k ₊ und k ₋ in einem Verschlingungs-Diagramm folgendermaßen definiert (siehe Abbildung für die Konvention für positive und negative Kreuzungen):

$lk(J,K)=\frac {k_+ - k_-}{2}$.

Literatur

• Charles Livingston: Knotentheorie für Einsteiger. Vieweg, Braunschweig u. a. 1995, ISBN 3-528-06660-1 (Vieweg Mathematik).