Clusterkoeffizient

Der Clusterkoeffizient (engl. clustering coefficient) ist in der Graphentheorie ein Maß für den Grad der Verlinkung in einem Graphen. Man unterscheidet den lokalen Clusterkoeffizienten für einen bestimmten Knoten des Graphen und den globalen Clusterkoeffizienten für den gesamten Graphen (auch Vernetzungsgrad).

Der lokale Clusterkoeffizient eines Knotens i in einem Graphen G bezeichnet in der Graphentheorie den Quotienten aus der Anzahl der Kanten, die zwischen seinen k_i Nachbarn tatsächlich verlaufen (n), und der Anzahl Kanten, die zwischen diesen Nachbarn maximal verlaufen können ($\tfrac{1}{2} k_i (k_i-1)$). Der Clusterkoeffizient C_i eines Knotens i berechnet sich daher wie folgt:

$C_i = \frac{2n}{k_i (k_i-1)}.$

Graph mit sechs Knoten

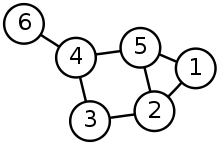
In dem nebenstehenden Graph hat der Knoten 1 die Nachbarn 2 und 5. Zwischen diesen Nachbarn ist eine Kante möglich und auch vorhanden, so dass der Clusterkoeffizent C₁ = 1 ist. Der Knoten 2 hat 3 Nachbarn, zwischen denen 3 Kanten möglich sind, jedoch sind nur die Nachbarknoten 1 und 5 durch eine Kante verbunden. Der Clusterkoeffizent C₂ ist daher $\tfrac{1}{3}$.

Der Clusterkoeffizient von Knoten 6, also sämtlicher Knoten des Grades 1, ergibt laut Berechnung die Division Null durch Null. Dies ist in der - JUNG-Bibliothek mit dem Wert 1 umgesetzt und resultiert in unnatürlich hohen globalen Clusterkoeffizienten, wenn viele Knoten den Grad 1 haben.

Der globale Clusterkoeffizient gibt das Verhältnis der vorhandenen Links zu den möglichen Links an. Ein vollständiger Graph, in dem jeder Knoten mit jedem verbunden ist, hat den maximal möglichen Clusterkoeffizient 1. Der globale Clusterkoeffizient lässt sich auch als Mittelwert der lokalen Clusterkoeffizienten aller Knoten berechnen.

Kleine-Welt-Netzwerke haben einen sehr hohen durchschnittlichen Clusterkoeffizienten. In einem Zufallsgraphen ist der Clusterkoeffizient im Gegensatz zu natürlichen Netzwerken relativ gering.

Siehe auch

Clusteranalyse, Vernetzung