CoNP

Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung.

In der Komplexitätstheorie bezeichnet Co-NP eine Komplexitätsklasse. In ihr sind genau die Sprachen enthalten, deren Komplemente zu NP gehören, d. h. 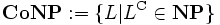$\mathbf{CoNP}:=\{L | L^{\rm C}\in\mathbf{NP}\}$. Intuitiv gesprochen besteht Co-NP aus der Klasse der Sprachen, in denen der Beweis, dass ein Wort nicht zur Sprache gehört, nichtdeterministisch polynomiell ist.

Zum Beispiel ist Subset Sum ein NP-vollständiges Problem. Gefragt ist, ob es in einer endlichen Menge ganzer Zahlen eine nichtleere Teilmenge gibt, deren Elemente c als Summe haben. Das Gegenstück in Co-NP ist die Frage, ob alle nichtleeren Teilmengen nicht c als Summe haben.

Beziehung zu anderen Komplexitätsklassen

P ist eine Teilmenge von sowohl NP als auch Co-NP. Es wird angenommen, dass in beiden Fällen eine echte Teilmengenbeziehung vorliegt. Man vermutet außerdem, dass 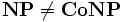$\mathbf{NP}\neq\mathbf{CoNP}$. Tatsächlich gilt folgender Satz: Wenn A NP-vollständig ist, dann ist 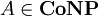$A\in\mathbf{CoNP}$ genau dann, wenn 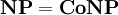$\mathbf{NP}=\mathbf{CoNP}$. Der nicht-triviale Teil der Äquivalenz kann wie folgt gezeigt werden:

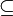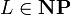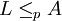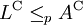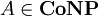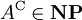$\subseteq$: Sei $L\in\mathbf{NP}$. Weil A NP-schwer ist, ist $L\leq_pA$, und damit $L^{\mathrm{C}}\leq_pA^{\mathrm{C}}$. Wegen $A\in\mathbf{CoNP}$ ist $A^{\mathrm{C}}\in\mathbf{NP}$, und damit ist 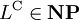$L^{\mathrm{C}}\in\mathbf{NP}$, also $L\in\mathbf{CoNP}$.

$\supseteq$: $L\in\mathbf{CoNP} \Rightarrow L^{\mathrm{C}}\in\mathbf{NP} \Rightarrow L^{\mathrm{C}}\in\mathbf{CoNP} \Rightarrow (L^{\mathrm{C}})^{\mathrm{C}}=L \in\mathbf{NP}$

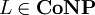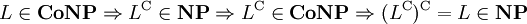
Ganz analog lässt sich folgender Satz zeigen: Wenn A Co-NP-vollständig ist, dann ist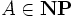 $A\in\mathbf{NP}$ genau dann, wenn $\mathbf{NP}=\mathbf{CoNP}$.

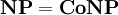Weil P unter Komplement abgeschlossen ist, gilt folgender Satz: Wenn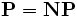 $\mathbf{P}=\mathbf{NP}$, dann 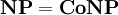$\mathbf{NP}=\mathbf{CoNP}$. Ob hiervon auch die Umkehrung gilt, ist unbekannt.

Wenn ein Problem sowohl in NP als auch in Co-NP enthalten ist, so wird allgemein angenommen, dass es nicht NP-vollständig ist (da ansonsten $\mathbf{NP} = \mathbf{CoNP}$).

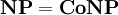Primzahltest

Lange Zeit wurde vermutet, dass Primalität im Durchschnitt von NP und Co-NP liegt, aber nicht zu P gehört.

2002 wurde von Manindra Agrawal, Neeraj Kayal und Nitin Saxena der Beweis erbracht, dass es in polynomieller Zeit (genauer in 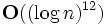$\mathbf{O}((\log n)^{12})$ möglich ist, zu entscheiden, ob eine vorgelegte Zahl prim ist oder nicht. Der AKS-Primzahltest liefert jedoch keine Primfaktorzerlegung.