Komplexitätsklasse NP

NP (nichtdeterministisch polynomielle Zeit) ist eine Komplexitätsklasse aus dem Bereich der Komplexitätstheorie. Sie bezeichnet die Klasse aller Entscheidungsprobleme, die von einer nichtdeterministischen Turingmaschine bezüglich der Eingabelänge in Polynomialzeit entschieden werden können.

Viele Probleme, die in der Komplexitätsklasse NP liegen, genauer gesagt die NP-vollständigen Probleme, lassen sich vermutlich nicht effizient lösen. Alle bekannten deterministischen Algorithmen für diese Probleme erfordern exponentiellen Rechenaufwand, und es wird vermutet, dass es keine effizienteren Algorithmen gibt. Die Bestätigung oder Widerlegung dieser Vermutung ist das P-NP-Problem, eines der wichtigsten offenen Probleme der Informatik.

Das vielleicht bekannteste NP-vollständige Problem ist das Problem des Handlungsreisenden.

Gelegentlich wird NP irrtümlich als die Klasse der nicht in Polynomialzeit lösbaren Probleme bezeichnet. Dies ist jedoch falsch: NP definiert lediglich eine obere Schranke für die Komplexität der enthaltenen Probleme, enthält aber auch die in Polynomialzeit lösbaren Probleme.

Äquivalente Charakterisierungen

Nach einer alternativen Definition ist ein Entscheidungsproblem genau dann in NP, wenn eine gegebene Lösung für das entsprechende Suchproblem von einer deterministischen Turingmaschine in Polynomialzeit überprüft werden kann. Im deutschen Sprachraum hat diese Definition den Vorteil, dass sich der Ausdruck NP-Problem auch als Nachweis-polynomielles Problem lesen lässt, das heißt, der Nachweis einer positiven Antwort kann in polynom-beschränkter Zeit vollzogen werden.

Eine weitere Charakterisierung von NP gibt es in der deskriptiven Komplexitätstheorie. Nach dem Satz von Fagin ist eine Sprache L genau dann in NP, wenn es einen Satz in der existenziellen Logik zweiter Stufe (SO∃) gibt, der L beschreibt.

Formale Definition

Von beiden Charakterisierungen kann man eine formale Definition wie folgt angeben:

Sprachakzeptanz-Definition

Eine Sprache L ist in NP, falls es eine nicht-deterministische Turingmaschine M und ein Polynom p gibt, sodass:

• Bei Eingabe von x hält M nach höchstens p( | x | ) Schritten (daher jeder Lauf von M auf x hat maximal Länge p( | x | ))
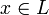• $x \in L$ genau dann wenn es mindestens einen akzeptierenden Lauf von M auf x gibt.

Suchproblem-Definition

Eine Sprache L ist in NP, falls es eine Relation 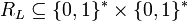$R_L \subseteq \{0,1\}^* \times \{0,1\}^*$ und ein Polynom p gibt, sodass:

• R_L wird von einer (deterministischen) Turingmaschine erkannt, und
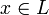• $x \in L$ genau dann, wenn es y gibt mit 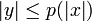$|y| \leq p(|x|)$ und $(x,y) \in R_L$.

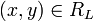Hierbei wird y auch ein "Beweis" (proof) oder ein "Zeuge" (witness) für x genannt, daher auch der (engl.) Name "witness relation" für die Relation R_L.

Äquivalenz der Definitionen

Gibt es eine NTM M, die L erkennt, so gibt es zu jedem 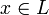$x \in L$ eine akzeptierende Rechnung von M, welche sich in einen String α_M(x) kodieren lässt. Die Relation R_L ist dann R_L = (x,α_M(x)) für alle 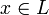$x \in L$ und erfüllt die obigen Eigenschaften, denn die akzeptierende Rechnung ist polynomiell in der Länge von x beschränkt und kann deterministisch polynomiell überprüft werden.

Gibt es umgekehrt eine Relation R_L nach obiger Definition, so kann eine NTM M konstruiert werden, die ein entsprechendes y zunächst nichtdeterministisch rät, und dann mittels einer DTM für R_L überprüft, ob 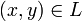$(x,y) \in L$, also $x \in L$.

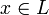Beziehung zu anderen Komplexitätsklassen

Die Klasse der Entscheidungsprobleme, deren Komplemente in NP liegen, wird mit CoNP bezeichnet. NP und CoNP sind nicht disjunkt, es ist jedoch unklar, ob NP=coNP gilt. (Es würde jedoch aus P=NP folgen, da P=coP.)

Meist sind für Beziehungen zwischen Komplexitätsklassen nur Inklusionsrelationen bekannt. Nicht bekannt ist, ob jeweils eine echte Teilmengenbeziehung gilt:

L ⊆ NL ⊆ LOGCFL ⊆ NC ⊆ P ⊆ NP ⊆ PSPACE = NPSPACE ⊆ EXPTIME ⊆ NEXPTIME

Die folgenden echten Inklusionen sind bekannt:

LOGCFL ⊂ PSPACE

P ⊂ EXPTIME

Q ⊂ NP

Eigenschaften von NP

Die Klasse NP ist abgeschlossen unter

• Vereinigung
• Durchschnitt
• Konkatenation
• Kleene-Stern
• epsilon-freien Homomorphismen
• inversen Homomorphismen

Offene Probleme

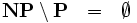• $\mathbf{NP}\setminus \mathbf{P} \,\,\,\,=\,\,\,\, \emptyset$? (P-NP-Problem)
• $\mathbf{PSPACE}\setminus \mathbf{NP} \,\,\,\,=\,\,\,\, \emptyset$?
• $\mathbf{EXPTIME}\setminus\mathbf{NP} \,\,\,\,=\,\,\,\, \emptyset$?
• $\mathbf{NP}\setminus \mathbf{CoNP} \,\,\,\,=\,\,\,\, \emptyset$?

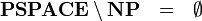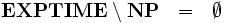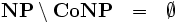Bekannte Probleme in NP

• Karps 21 NP-vollständige Probleme
• SAT ist NP-vollständig.
• Das Cliquenproblem ist NP-vollständig.
• Das Hamiltonkreisproblem ist NP-vollständig.
• Das Rucksackproblem ist NP-vollständig.

Siehe auch

• NP-Schwere

Weblinks

• NP im Complexity Zoo (englisch)
• Vorlesungsreihe zur "Komplexitätstheorie", Prof. Dr. Christoph Meinel, Hasso-Plattner-Institut (Sommersemester 2008)

Quellen

• Christos H. Papadimitriou: Computational Complexity. Addison Wesley, ISBN 978-0201530827