Coding Gain

Dieser Artikel wurde auf der Qualitätssicherungsseite des Portals Mathematik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Mathematik auf ein akzeptables Niveau zu bringen. Dabei werden Artikel gelöscht, die nicht signifikant verbessert werden können. Bitte hilf mit, die Mängel dieses Artikels zu beseitigen, und beteilige dich bitte an der Diskussion!

Der Codegewinn, auch Codierungsgewinn, beschreibt in der Codierungstheorie die Differenz der benötigten Bitenergie im Verhältnis zur spektralen Rauschleistungsdichte zwischen einer uncodierten und codierten Nachricht um die gleiche Bitfehlerrate zu erreichen. Die uncodierte Nachricht stellt die Referenz dar, mit der die mittels Kanalcodierung codierende Nachricht verglichen wird.

Die Codierung einer Nachricht wird in diesem Kontext immer durch die Kanalcodierung bewerkstelligt, welche die Aufgabe hat, durch Hinzufügen redundanter Information mehr Sicherheit vor z.B. Übertragungs- oder Speicherfehlern zu gewährleisten. Fehlerursachen können dabei Störungen sein wie sie beispielsweise durch Rauschen ausgelöst werden.

Der Einfluss der Fehlergröße wird in der Codierungstheorie durch das Bitenergie-Rauschleistungsdichte-Verhältnis 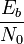$\frac{E_b}{N_0}$ausgedrückt, welches das Verhältnis der für ein Informationsbit aufgewendeten Energie E_b zu der spektralen Rauschleistungsdichte N₀ darstellt.

Der Codegewinn C (in dB) ergibt sich zu:

$C = \frac{E_b}{N_0}|_{uncodiert} - \frac{E_b}{N_0}|_{codiert}$.

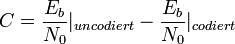Die Bitenergie E_b ist normiert und berücksichtigt, dass bei der codierten Übertragung redundante Bits übertragen werden.

Rauschen und Codierung beeinflussen die Bitfehlerhäufigkeit bei der Informationsübertragung.