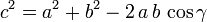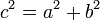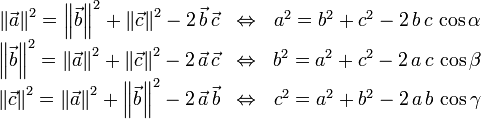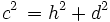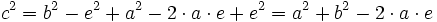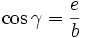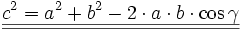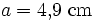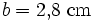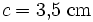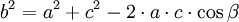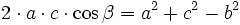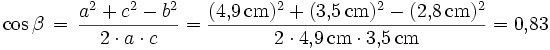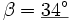Cosinussatz

In der Trigonometrie stellt der Kosinussatz eine Beziehung zwischen den drei Seiten eines Dreiecks und dem Kosinus eines der drei Winkel des Dreiecks her.

Für die drei Seiten a, b und c eines Dreiecks sowie für den der Seite c gegenüberliegenden Winkel – d.h. den von den Vektoren $\vec a$ und $\vec b$ eingeschlossenen Winkel – γ gilt:

$c^2=a^2+b^2-2\,a\,b\,\cos\gamma$

Folgerungen

Aus dem Kosinussatz kann man einige wichtige Folgerungen schließen. Hier sind insbesondere der Satz des Pythagoras und die Kongruenzsätze von Bedeutung.

Satz des Pythagoras

Mit

$\gamma = 90^{\circ} = \frac{\pi}{2}$

also bei einem rechtwinkligen Dreieck, gilt

$\cos\gamma = \cos\frac{\pi}{2} = 0$.

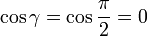Dadurch ergibt sich als Spezialfall des Kosinussatzes im rechtwinkligen Dreieck der Satz des Pythagoras:

$c^2=a^2+b^2\,$

Kongruenzsätze

Die Kongruenzsätze SSS (Seite-Seite-Seite) und SWS (Seite-Winkel-Seite) besagen, dass ein Dreieck durch die Vorgabe von drei Seiten oder von zwei Seiten und ihrem Zwischenwinkel vollständig bestimmt ist. Alternativ kann man auch jeweils zwei Vektoren angeben, aus denen der eingeschlossene Winkel berechnet werden kann. Der Kosinussatz erlaubt es in diesen Fällen, aus den drei gegebenen Stücken ein viertes Stück, nämlich einen Winkel (im Fall SSS) beziehungsweise die dritte Seite (im Fall SWS) zu berechnen. Wenn man anschließend auch die übrigen Winkel eines Dreiecks ermitteln möchte, kann man wahlweise nochmal den Kosinussatz (mit auf den gesuchten Winkel angepassten Seitenbezeichnungen) oder den Sinussatz anwenden. Den letzten Winkel berechnet man am zweckmäßigsten über die Winkelsumme von 180°.

Die Formeln für das allgemeine Dreieck lauten wie folgt:

$\begin{array}{ccc} \left\|\vec{a}\right\|^2=\left\|\vec{b}\right\|^2+\left\|\vec{c}\right\|^2-2\,\vec{b}\,\vec{c} &\Leftrightarrow&a^2=b^2+c^2-2\,b\,c\,\cos\alpha\\ \left\|\vec{b}\right\|^2=\left\|\vec{a}\right\|^2+\left\|\vec{c}\right\|^2-2\,\vec{a}\,\vec{c} &\Leftrightarrow&b^2=a^2+c^2-2\,a\,c\,\cos\beta\\ \left\|\vec{c}\right\|^2=\left\|\vec{a}\right\|^2+\left\|\vec{b}\right\|^2-2\,\vec{a}\,\vec{b} &\Leftrightarrow&c^2=a^2+b^2-2\,a\,b\,\cos\gamma \end{array}$

wobei es sich hierbei jeweils eine Umformung des Kosinussatzes für die jeweiligen Bezugswinkel (bzw. Bezugsvektoren) handelt.

Wenn nur eine Seite und zwei Winkel gegeben sind (Kongruenzsätze SWW oder WSW) oder zwei Seiten und der Gegenwinkel der größeren Seite (Kongruenzsatz SsW), so berechnet man zunächst eines der fehlenden Stücke mit dem Sinussatz und den fehlenden Winkel über die Winkelsumme, bevor man mit dem Kosinussatz die dritte Seite bestimmen kann.

Beweis

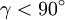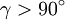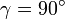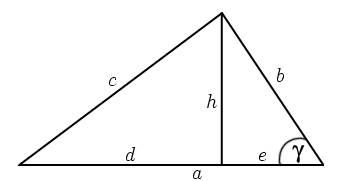
Im folgenden Beweis wird $\gamma < 90^\circ$ vorausgesetzt. Für $\gamma > 90^\circ$ muss der Beweis geringfügig modifiziert werden. Für $\gamma = 90^\circ$ ergibt sich der Kosinussatz direkt aus dem Satz des Pythagoras.

In den Teildreiecken soll der Satz des Pythagoras angewandt werden, um einen Rechenausdruck für c² zu finden. Dazu benötigt man die Quadrate der Kathetenlängen dieses Teildreiecks:

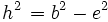$h^2 \,= b^2 - e^2$ (Satz des Pythagoras für das rechte Teildreieck)

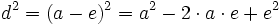$d^2 = (a-e)^2 = a^2 - 2 \cdot a \cdot e + e^2$ (binomische Formel)

Nach Pythagoras gilt für das linke Teildreieck:

$c^2 \,= h^2 + d^2$

Es müssen also die beiden oben gefundenen Rechenausdrücke addiert werden:

$c^2 = b^2 - e^2 + a^2 - 2 \cdot a \cdot e + e^2 = a^2 + b^2 - 2 \cdot a \cdot e$

Nun gilt aber

$\cos \gamma = \frac{e}{b}$ $\left(=\frac{\rm Ankathete}{\rm Hypotenuse}\right)$

mit der Folgerung

$e = b \cdot \cos\gamma$.

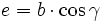Einsetzen dieses Zwischenergebnisses in die Gleichung für c² ergibt die Behauptung:

$\underline{\underline{c^2 = a^2 + b^2 - 2 \cdot a \cdot b \cdot \cos \gamma}}$

Anwendungsbeispiel

Die folgenden Zahlenwerte sind grobe Näherungen. Gegeben sei ein Dreieck ABC, bei dem die Längen aller drei Seiten bekannt sind.

$a = 4{,}9\;\rm cm$

$b = 2{,}8\;\rm cm$

$c = 3{,}5\;\rm cm$

Gesucht ist die Winkelgröße β (Bezeichnungen wie üblich).

$b^2 = a^2 + c^2 - 2 \cdot a \cdot c \cdot \cos \beta$

$2 \cdot a \cdot c \cdot \cos \beta = a^2 + c^2 - b^2$

$\cos \beta \, = \, \frac{a^2 + c^2 - b^2}{2 \cdot a \cdot c} = \frac{(4{,}9\,{\rm cm})^2 + (3{,}5\,{\rm cm})^2 - (2{,}8\,{\rm cm})^2} {2 \cdot 4{,}9\,{\rm cm} \cdot 3{,}5\,{\rm cm}} = 0{,}83$

$\beta = \underline{34^\circ}$

Siehe auch

• Satz des Pythagoras
• Kosinus
• Sinussatz
• Sinus

Weblinks

• Dreiecksberechnung - Rechner mit Anzeige des Rechenweges