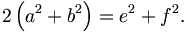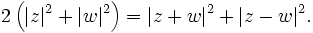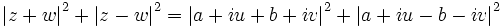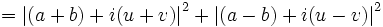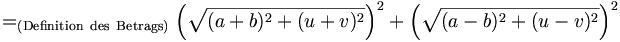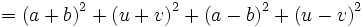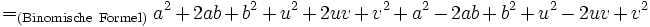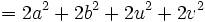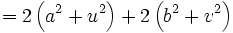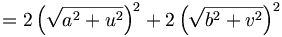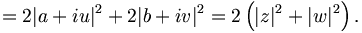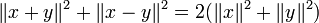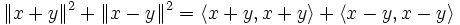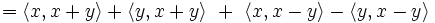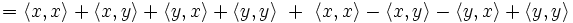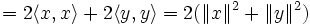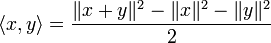Parallelogrammidentität

Die Parallelogrammgleichung (oder Parallelogrammgesetz) ist ein mathematischer Satz, der seine Ursprünge und seinen Namen von der elementaren Geometrie hat, aber in sehr ähnlicher Formulierung auch für komplexe Zahlen und Vektoren in Innenprodukträumen gilt.

Anwendung in der Geometrie

Satz

In einem Parallelogramm gilt mit den Seitenlängen a, b und den Diagonalen e, f:

$2\left(a^2+b^2\right)=e^2+f^2.$

Bezeichnungen am Parallelogramm

Beweis

Der Beweis ist mit dem Cosinussatz sehr einfach:

$e^2+f^2 = (a^2+b^2-2ab\ \cos(\beta))+(c^2+b^2-2cb\ \cos(\gamma)) = 2(a^2+b^2)$,

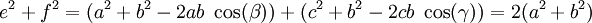da c = a und cos(γ) = cos(π − β) = − cos(β) ist.

Anwendung für komplexe Zahlen

Satz

Für zwei komplexe Zahlen z,w gilt:

$2\left(|z|^2+|w|^2\right) = |z+w|^2 + |z-w|^2.$

Beweis

Die Gültigkeit des Satzes ist offensichtlich, wenn man die Zahlen in der Gauß'schen Zahlenebene interpretiert, in der z und w dann ein Parallelogramm mit den Diagonalen z+w und z-w aufspannen. Trotzdem soll an dieser Stelle ein kurzer Beweis geliefert werden, der den Satz elementar herleitet. Es seien $z,w \in \mathbb{C}, z=a+iu, w=b+iv.$ Dann gilt:

$\left|z+w\right|^2 + \left|z-w\right|^2 = \left|a+iu+b+iv\right|^2 + \left|a+iu-b-iv\right|^2$

$=\left|(a+b)+i(u+v)\right|^2 + \left|(a-b)+i(u-v)\right|^2$

$=_{\mathrm{(Definition\ des\ Betrags)}} \left(\sqrt{(a+b)^2+(u+v)^2}\right)^2+\left(\sqrt{(a-b)^2+(u-v)^2}\right)^2$

$= \left(a+b\right)^2+\left(u+v\right)^2+\left(a-b\right)^2+\left(u-v\right)^2$

$=_{\mathrm{(Binomische\ Formel)}} a^2+2ab+b^2+u^2+2uv+v^2 + a^2-2ab+b^2+u^2-2uv+v^2$

$= 2a^2 + 2b^2 + 2u^2 + 2v^2\;$

$= 2\left(a^2 + u^2\right) + 2\left(b^2 + v^2\right)$

$= 2 \left(\sqrt{a^2 + u^2} \right)^2 + 2 \left(\sqrt{b^2 + v^2} \right)^2$

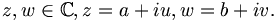$= 2 |a+iu|^2 + 2 |b+iv|^2 = 2\left(|z|^2+|w|^2\right).$

Die Gleichung in Vektorräumen

Die Betrachtung in Prähilberträumen stellt die am meisten abstrahierte Betrachtung dar. Selbstverständlich lassen sich die Aussagen der beiden vorhergehenden Abschnitte mit dem nun folgenden Satz beweisen (zum einen mit den Mitteln der analytischen Geometrie, zum anderen durch die Zurückführung von $\mathbb{C}$ auf einen zweidimensionalen $\mathbb{R}$-Vektorraum unter Definition einer Multiplikation und einer Norm), dennoch sind die jeweiligen Beweise mit den je zur Verfügung stehenden Mitteln sicher nicht überflüssig.

Satz

In Prähilberträumen, also Vektorräumen, in denen ein Skalarprodukt definiert ist, (oder in Vektorräumen mit zumindest einem positiv semidefiniten inneren Produkt) gilt:

$\|x+y\|^2+\|x-y\|^2=2(\|x\|^2+\|y\|^2)$

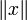wobei $\|x\|$ die Norm (Seminorm) und 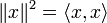$\|x\|^2 = \langle x, x\rangle$ das Skalarprodukt (positiv semidefinite innere Produkt) ist.

Beweis

Zum Beweis benötigt man nur die Tatsache, dass ein Innenprodukt eines jeden Innenproduktraums bezüglich der Addition für beide Argumente linear ist (siehe Definition des Innenprodukts und Sesquilinearform). Dann erhält man:

$\|x+y\|^2+\|x-y\|^2 = \langle x+y, x+y\rangle + \langle x-y, x-y\rangle$

$= \langle x, x+y\rangle +\langle y, x+y\rangle \ +\ \langle x, x-y\rangle - \langle y, x-y\rangle$

$= \langle x, x \rangle +\langle x, y\rangle + \langle y, x \rangle +\langle y, y\rangle \ +\ \langle x, x\rangle - \langle x, y\rangle - \langle y, x\rangle + \langle y, y\rangle$

$= 2\langle x, x \rangle + 2\langle y, y\rangle = 2(\|x\|^2+\|y\|^2)$

Gültigkeit für normierte Räume ohne Innenprodukt

Da ein normierter Raum keineswegs notwendigerweise ein Innenprodukt besitzt, jedoch nach seiner Definition eine Norm, stellt sich die Frage, ob der Satz nicht auch für alle normierten Räume gilt. (In Innenprodukträumen ist die Norm immer die Wurzel des inneren Produkts, aber nicht in allen normierten Räumen)

Interessanterweise gilt der Satz nur für die Räume, in denen die Norm auf die übliche Weise aus einem Innenprodukt hervorgeht, denn wenn man die Gültigkeit voraussetzt, dann ist durch

$\langle x, y\rangle={\|x+y\|^2-\|x\|^2-\|y\|^2\over 2}$

"automatisch" ein inneres Produkt definiert, dessen Norm genau diese Eigenschaft erfüllt.

Weblinks