Cubus simus

Abgeschrägtes Hexaeder

Das abgeschrägte Hexaeder (auch Cubus simus genannt) ist ein chirales Polyeder, das zu den Archimedischen Körpern zählt. Es setzt sich aus 38 Flächen, nämlich 6 Quadraten und 32 gleichseitigen Dreiecken, zusammen und hat 24 Ecken sowie 60 Kanten. Dabei bilden jeweils vier Dreiecke und ein Quadrat eine Raumecke.

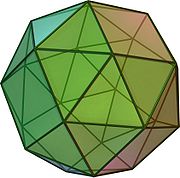
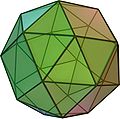
Die jeweils sich paarweise gegenüberliegenden Quadrate sind parallel und gegeneinander um ca. 33° verdreht (die Drehachse verläuft durch die Flächenmitten). Die folgenden Bilder zeigen zwei zueinander spiegelbildliche abgeschrägte Hexader.

Spiegelvariante 1

Spiegelvariante 2

Konstruktion

»Schiefes« Dekaeder mit 8 Fünfecken und 2 Quadraten als Begrenzungsflächen.

• Wie der Name schon andeutet, entsteht dieses Polyeder durch fortwährendes Abschrägen eines Hexaeders, sodass am Ende sechs (kleinere) Quadrate übrigbleiben, die koinzident mit den ursprünglichen Begrenzungsflächen des Würfels sind.

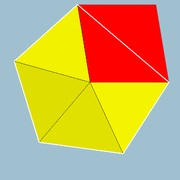
• Durch das Aufsetzen kleiner Pyramiden (mit fünfeckiger Grundfläche und vier gleichseitigen Dreiecken sowie einem „halben Quadrat“ als Mantelfläche) auf die acht fünfeckigen Begrenzungsflächen eines speziellen Dekaeders (s. Abb. rechts) erhält man ebenfalls ein abgeschrägtes Hexaeder.

• Verdreht man bei einem Rhombenkuboktaeder diejenigen sechs Quadrate, die koinzident mit den Begrenzungsflächen eines umbeschriebenen Würfels sind (und sich paarweise gegenüberliegen), gegeneinander um den Winkel ω (s. Formel unten) und fügt jeweils eine Diagonale in die übrigen, jetzt verzerrten Quadrate ein, entsteht auch ein abgeschrägtes Hexaeder.

Formeln

Ausschnitt einer Raumecke des abgeschrägten Hexaeders.

Nachfolgend bezeichne der Term t den Kosinus des kleineren Zentriwinkels ζ im Sehnenfünfeck (die weißen Linien in der Grafik rechts) mit den Seitenlängen a und d (Quadratdiagonale).

$t = cos(\zeta) = \frac{1}{6} \left(\sqrt[3]{19 + 3\sqrt{33}} + \sqrt[3]{19 - 3\sqrt{33}} -2 \right)$

Wird zum doppelten Wert von t die Zahl 1 addiert, erhält man die Tribonacci-Konstante, welche den Limes des Verhältnisses (≈ 1,84) zweier aufeinanderfolgenden Zahlen dieser Folge darstellt.

Größen eines abgeschrägten Hexaeders mit Kantenlänge a
Oberflächeninhalt	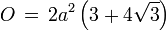$O \, = \, 2a^2 \left(3 + 4 \sqrt{3} \right)$
Volumen	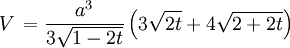$V \, = \frac{a^3}{3\sqrt{1-2t}} \left(3\sqrt{2t} + 4\sqrt{2+2t}\right)$
Umkugelradius	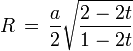$R \, = \, \frac{a}{2} \sqrt{\frac{2-2t}{1-2t}}$
Kantenkugelradius	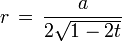$r \, = \, \frac{a}{2\sqrt{1- 2t}}$
Flächen-Flächen-Winkel ≈ 153,24° (Trigon–Trigon)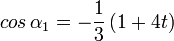	$cos \, \alpha_1 = -\frac{1}{3}\left(1+4t\right)$
Flächen-Flächen-Winkel ≈ 137,9° (Quadrat–Trigon)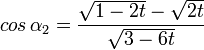	$cos \, \alpha_2 = \frac{\sqrt{1-2t}-\sqrt{2t}}{\sqrt{3-6t}}$
Flächen-Kanten-Winkel ≈ 126,4° (Quadrat–Trigon)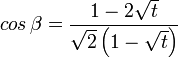	$cos \, \beta = \frac{1-2\sqrt{t}}{\sqrt{2}\left(1-\sqrt{t}\right)}$
Kanten-Kanten-Winkel ≈ 114,81° (Trigon–Trigon)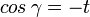	$cos \, \gamma = -t$
Quadrat-Drehwinkel ≈ 32,94°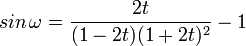	$sin \, \omega = \frac{2t}{(1-2t)(1+2t)^2} -1$

Weblinks

• Eric W. Weisstein: Snub Cube auf MathWorld

Platonische Körper

Tetraeder | Würfel | Oktaeder | Dodekaeder | Ikosaeder

 

Archimedische Körper

Tetraederstumpf · Kuboktaeder · Hexaederstumpf · Oktaederstumpf · Rhombenkuboktaeder · Großes Rhombenkuboktaeder · Dodekaederstumpf · Ikosaederstumpf · Ikosidodekaeder · Abgeschrägtes Hexaeder · Rhombenikosidodekaeder · Großes Rhombenikosidodekaeder · Abgeschrägtes Dodekaeder 

 

Catalanische Körper

Rhombendodekaeder · Triakistetraeder · Triakisoktaeder · Tetrakishexaeder · Deltoidalikositetraeder · Pentagonikositetraeder · Rhombentriakontaeder · Hexakisoktaeder · Triakisikosaeder · Pentakisdodekaeder · Deltoidalhexakontaeder · Pentagonhexakontaeder · Disdyakistriakontaeder