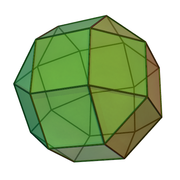
Archimedische Körper

Die archimedischen Körper sind eine Klasse von sehr regelmäßigen geometrischen Körpern, die den platonischen Körpern ähneln. Je nach Zählweise gibt es 13 oder 15 archimedische Körper. Sie zeichnen sich dadurch aus, dass die Ecken eines solchen Körpers nicht voneinander unterschieden werden können. Sie sind nach dem griechischen Mathematiker Archimedes benannt, der alle diese Körper bereits im dritten Jahrhundert vor Christus entdeckt hatte. Die Schrift des Archimedes ist nicht erhalten, es ist nur eine Zusammenfassung des alexandrinischen Mathematikers Pappos (4. Jahrhundert nach Christus) überliefert^[1].

Definition

Informelle Beschreibung

Die archimedischen Körper sind konvexe Polyeder (Vielflächner), deren Seitenflächen regelmäßige Vielecke sind. Die charakteristische Eigenschaft der archimedischen Körper ist, dass sich alle Ecken des Körpers zueinander völlig gleich verhalten (Uniformität der Ecken). Dabei treten einige einfache Fälle auf, die man schon unter anderen Namen kennt, nämlich Prismen, Antiprismen und die fünf platonischen Körper. Diese werden nicht als archimedische Körper bezeichnet.

Die exakte Definition der Uniformität der Ecken bereitet einige Mühe und war in der Vergangenheit nicht immer einheitlich.

Exakte Definition

Zunächst betrachtet man alle konvexen Polyeder, deren Seitenflächen regelmäßige Polygone sind, und die die globale Uniformität der Ecken erfüllen:

Die Symmetriegruppe des Polyeders operiert transitiv auf seinen Ecken.

Das bedeutet anschaulich:

Zu jedem Paar (a,b) von Ecken des Polyeders ist es möglich, das Polyeder so zu drehen und zu spiegeln, dass die Ecke a dort zu liegen kommt, wo zuvor die Ecke b war, und die beiden Positionen des Polyeders vor und nach der Drehung nicht zu unterscheiden sind.

Es gibt mehrere einfache Klassen von konvexen Polyedern, die alle diese Eigenschaften erfüllen:

• Die fünf platonischen Körper.
• Alle Prismen, die aus genau zwei kongruenten regelmäßigen n-Ecken und n Quadraten bestehen. Zu jeder natürlichen Zahl n größer gleich drei existiert ein solches Prisma. An einer Ecke treffen stets ein n-Eck und zwei Quadrate zusammen. Im Fall n = 4 ergibt sich ein Würfel, also ein platonischer Körper.
• Alle Antiprismen, die aus genau zwei kongruenten n-Ecken und 2n gleichseitigen Dreiecken bestehen. Zu jeder natürlichen Zahl n größer gleich drei existiert ein solches Antiprisma. An einer Ecke treffen stets ein n-Eck und drei Dreiecke zusammen. Im Fall n = 3 ergibt sich ein Oktaeder, also ein platonischer Körper.

Die archimedischen Körper sind nun definiert als alle konvexen Polyeder mit regelmäßigen Seitenflächen, die die globale Uniformität der Ecken erfüllen und nicht in eine dieser drei genannten Klassen fallen.

Eigenschaften

• Unterscheidet man nicht zwischen ähnlichen Körpern, so existieren genau 13 archimedische Körper. Von zwei dieser Körper existieren je zwei spiegelbildlich entgegengesetzte Varianten, welche nicht durch Drehung ineinander übergeführt werden können. Diese werden gelegentlich doppelt gezählt, so dass sich nach dieser Zählweise dann insgesamt 15 archimedische Körper ergeben.
• Weil die Seitenflächen regelmäßige Polygone sind, gilt: Alle Kanten eines archimedischen Körpers haben die gleiche Länge.
• Aus der globalen Uniformität der Ecken folgt die lokale Uniformität der Ecken:

An jeder Ecke treffen im Uhrzeigersinn oder im Gegenuhrzeigersinn abgelesen dieselben Typen von Polygonen zusammen.

• Aus der lokalen Uniformität der Ecken folgt jedoch im Allgemeinen nicht die globale Uniformität. Ein Gegenbeispiel liefert das Pseudo-Rhombenkuboktaeder.
• Die Flächenfolge an einer Ecke charakterisiert jeden archimedischen (sowie auch platonischen) Körper eindeutig.
• Die zu den archimedischen Körpern dualen Polyeder sind die catalanischen Körper. Die charakteristische Eigenschaft dieser Körper ist die Uniformität der Flächen, welche sich aus der Uniformität der Ecken der archimedischen Körper ergibt.
• Jeder archimedische Körper kann durch Abstumpfen aus einem platonischen Körper erzeugt werden. Bei vielen archimedischen Körpern deutet auch der Name darauf hin. Mit Abstumpfen eines Körpers ist hier gemeint, dass dem Körper beliebige Stücke weggeschnitten werden, dabei aber die Flächen des Körpers — in aller Regel verkleinert — als Flächen des abgestumpften Körpers erhalten bleiben.
• Wenn ein archimedischer Körper durch Abstumpfen aus einem platonischen Körper erzeugt werden kann, dann kann er auch aus dem dazu dualen platonischen Körper durch Abstumpfen erzeugt werden.

Die einzelnen archimedischen Körper

Name und Bild	Flächen	Kanten	Ecken	Flächenfolge an den Ecken	Symmetrie- gruppe
Kuboktaeder	14 (8 Dreiecke, 6 Quadrate)	24	12	(3,4,3,4) Dreieck–Quadrat–Dreieck–Quadrat	Oh
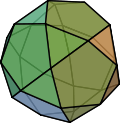
Ikosidodekaeder	32 (20 Dreiecke, 12 Fünfecke)	60	30	(3,5,3,5) Dreieck–Fünfeck–Dreieck–Fünfeck	Ih
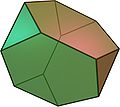
Tetraederstumpf	8 (4 Dreiecke, 4 Sechsecke)	18	12	(3,6,6) Dreieck–Sechseck–Sechseck	Td
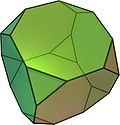
Hexaederstumpf	14 (8 Dreiecke, 6 Achtecke)	36	24	(3,8,8) Dreieck–Achteck–Achteck	Oh
Oktaederstumpf	14 (6 Quadrate, 8 Sechsecke)	36	24	(4,6,6) Quadrat–Sechseck–Sechseck	Oh
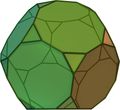
Dodekaederstumpf	32 (20 Dreiecke, 12 Zehnecke)	90	60	(3,10,10) Dreieck–Zehneck–Zehneck	Ih
Ikosaederstumpf oder Fußballkörper	32 (12 Fünfecke, 20 Sechsecke)	90	60	(5,6,6) Fünfeck–Sechseck–Sechseck	Ih
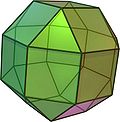
(Kleines) Rhombenkuboktaeder	26 (8 Dreiecke, 18 Quadrate)	48	24	(3,4,4,4) Dreieck–Quadrat–Quadrat–Quadrat	Oh
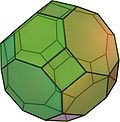
Großes Rhombenkuboktaeder oder Kuboktaederstumpf	26 (12 Quadrate, 8 Sechsecke, 6 Achtecke)	72	48	(4,6,8) Quadrat–Sechseck–Achteck	Oh
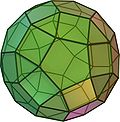
(Kleines) Rhombenikosidodekaeder	62 (20 Dreiecke, 30 Quadrate, 12 Fünfecke)	120	60	(3,4,5,4) Dreieck–Quadrat–Fünfeck–Quadrat	Ih
Großes Rhombenikosidodekaeder oder Ikosidodekaederstumpf	62 (30 Quadrate, 20 Sechsecke, 12 Zehnecke)	180	120	(4,6,10) Quadrat–Sechseck–Zehneck	Ih
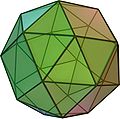
Abgeschrägtes Hexaeder oder Cubus simus (zwei spiegelbildlich entgegengesetzte Varianten)	38 (32 Dreiecke, 6 Quadrate)	60	24	(3,3,3,3,4) Dreieck–Dreieck–Dreieck–Dreieck–Quadrat	O
Abgeschrägtes Dodekaeder oder Dodecaedron simum (zwei spiegelbildlich entgegengesetzte Varianten)	92 (80 Dreiecke, 12 Fünfecke)	150	60	(3,3,3,3,5) Dreieck–Dreieck–Dreieck–Dreieck–Fünfeck	I

Das Pseudo-Rhombenkuboktaeder

Pseudo-Rhombenkuboktaeder

Lange Zeit benutzte man für die Definition der archimedischen Körper nicht die globale, sondern die anschaulichere lokale Uniformität der Ecken. Erst im Jahr 1930 stellte der britische Mathematiker J. C. P. Miller fest, dass ein konvexes Polyeder mit regelmäßigen Seitenflächen existiert, welches die lokale Uniformität der Ecken erfüllt, aber bisher nicht als archimedischer Körper erkannt worden war. Dieses Polyeder entsteht, wenn man beim Rhombenkuboktaeder eine Kappe um 45 Grad verdreht. Es wird als Pseudo-Rhombenkuboktaeder, als Miller's solid oder als Johnson-Körper J₃₇ bezeichnet.

In jeder Ecke dieses Körpers stoßen wie beim Rhombenkuboktaeder drei Quadrate und ein Dreieck zusammen, die lokale Uniformität der Ecken ist also gegeben. Im Gegensatz zu den klassischen archimedischen Körpern können trotzdem zwei verschiedene Typen von Ecken unterschieden werden. Dazu ist es aber notwendig, nicht nur die direkten Nachbarflächen der Ecke zu betrachten, sondern zur Unterscheidung auch die weiter entfernten Nachbarflächen der Ecke mit einzubeziehen.

Gelegentlich klassifiziert man das Pseudo-Rhombenkuboktaeder als 14. archimedischen Körper. In der Regel herrscht aber die Meinung vor, dass es aufgrund der unterschiedlichen Typen von Ecken nicht als archimedischer Körper angesehen werden sollte. Die Forderung der starken Uniformität der Ecken sorgt dann dafür, dass das Pseudo-Rhombenkuboktaeder aus der Definition ausgeschlossen wird.

Literatur

• Paul Adam, Arnold Wyss: Platonische und Archimedische Körper, ihre Sternformen und polaren Gebilde, ISBN 3-7725-0965-7

Weblinks

• Der Fußball als Archimedischer Körper

Einzelnachweise

1. ↑ Mathematicae collectiones V, 19