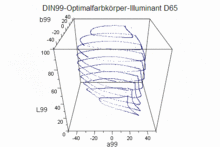
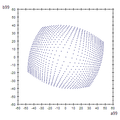
DIN99-Farbraum

	DIN 6176
Bereich	Farbmetrik
Titel	Farbmetrische Bestimmung von Farbabständen bei Körperfarben nach der DIN99-Formel
Kurzbeschreibung:	Farbraumsystem
Letzte Ausgabe	3.2001
ISO

Das DIN99-Farbraumsystem ist eine vom Arbeitsausschuss FNF/FNL 2 Farbmetrik erarbeitete Weiterentwicklung des CIELAB-Farbraumsystems. Die Berechnung ist in der DIN 6176:2001-03 Farbmetrische Bestimmung von Farbabständen bei Körperfarben nach der DIN99-Formel beschrieben. Dieser Farbraum wird auch in der ASTM-Norm (American Society for Testing and Materials) ASTM D 2244 aus 2007 Standard Practice for Calculation of Color Tolerances and Color Differences from Instrumentally Measured Color Coordinates zitiert.

Problem der Gleichabständigkeit

Grund dieser Entwicklung waren Mängel in der Berechnung der wahrnehmungsgerechten Gleichabständigkeit von Farbabständen des CIELAB-Farbraums. Auch die Unterbewertung von Farbabständen nahe der Unbuntachse und Schwächen in der Bewertung stark gesättigter Farben (hohe Chroma-Werte, besonders der Gelbtöne) sind weitere Unzulänglichkeiten des CIELAB-Farbraums. Der dritte Punkt, der eine Korrektur erfahren hat, ist die Tatsache, dass CIELAB die Helligkeitswerte (L*) unzulänglich bewertet. Um diese Mängel zu beheben, wurden von der CIE die Farbabstandsformeln CIE94 und CIEDE2000 entwickelt.

DIN99-Optimalfarbkörper in Schnittdarstellung. Schnittebenen von L₉₉=5 bis 95 in Zehnerschritten. Beleuchtungsquelle: D65

Anders als in den Systemen CIE94 und CIEDE2000 werden in DIN99 nicht die Farbabstandsformeln selbst modifiziert, sondern der gesamte Farbraum zu besserer Gleichabständigkeit transformiert. Das Ergebnis ist ein Farbraum, dessen Gestalt dem Ideal einer Kugel (vollständige Gleichabständigkeit) im Vergleich zu CIELAB recht nahe kommt.Die Darstellung von Gerätefarbräumen sieht durch die typische (transformationsbedingte) Wölbung ungewohnt aus, ermöglicht aber einen wahrnehmungsgetreueren Eindruck von der Farbraumgröße und -gestalt. Der DIN99-Farbraum selbst ist euklidisch (rechtwinklig). Die Wölbung der Farbraumdarstellung entsteht allein durch die transformierten CIELAB-Koordinaten. Deshalb bleibt die Berechnung des Farbabstandes unverändert. Sie wird durch den euklidischen Abstand ermittelt, wie in CIELAB.

Beschreibung

Basis des DIN99-Farbraumes ist der CIELAB-Farbraum mit seinen Koordinaten L ^* , a ^* , b ^* .

Die Transformation von CIELAB in DIN99 wird in zwei Teilen ausgeführt: Eine Helligkeitstransformation zur neuen DIN99-Helligkeit L₉₉ und eine Buntheits- oder Chroma-Transformation.

Nach den Transformationen können dann die Werte wie Chroma (C₉₉), Bunttonwinkel (h₉₉) und Farbabstand (ΔE₉₉) berechnet werden.

Anwendungsvoraussetzungen

Die DIN99-Formel ist für kleine bis mittlere Farbabstände konzipiert. Die Anwendung wird für Farbabstände bis 5 ΔE CIELAB empfohlen.

Betrachtungsbedingungen

Die Referenzbedingungen für die Bewertung lauten wie folgt (nach CIE-Publikationen 101 und 116):

• Illuminant D65
• 1000lx
• Umbgebungsfarbe 50 L* (CIELAB)
• Probengröße soll mehr als 4° des Gesichtsfeldes umfassen (entsprechend 10°-Standardbeobachter)
• Muster- und Vergleichsprobe möglichst homogen (ohne Struktur)
• Muster- und Vergleichsprobe direkt aneinander grenzend.
• Helligkeit des Musters im Bereich von 50 L* (CIELAB)
• Beobachter: farbnormalsichtig
• Erscheinungsweise: Körperfarbe
• Größe des Farbabstandes: unter 5 CIELAB-Einheiten

Berechnung

Helligkeitstransformation

Die Helligkeit L ^* wird zur DIN99-Helligkeit L₉₉ transformiert:

$L_{99}= (1/k_E) \cdot 105{,}51 \cdot \ln \left(1+0{,}0158 \cdot L^{*}\right)$

Diese Transformation soll die Unterscheidbarkeit dunkler Farbtöne besser wiedergeben. Die Transformation ähnelt einer Potenzfunktion mit einem Exponenten von 0,75. Der Bereich der dunklen Farbtöne wird gestreckt und der Bereich der hellen Farbtöne wird gestaucht. Mittlere Helligkeitswerte werden auf der Helligkeitsachse nach oben verschoben.

Die Variable k_E beschreibt den Einfluss geänderter Betrachtungsbedingungen, womit unter Referenzbedingungen k_E = 1 gilt.

Buntheitstransformation

Die Transformation der Buntheitskoordinaten findet in drei Schritten statt:

• Die Buntheitsachsen werden um 16° gedreht
• Die Gelb-Blau-Achse wird mit dem Faktor 0,7 multipliziert, also gestaucht
• Die Buntheitswerte (Chroma) werden radial um die L₉₉-Achse logarithmisch komprimiert

• 

  Ausgangssituation: a*/b*-Ebene. Die Punkte dieser und der folgenden Abbildungen stellen die a*/b*-Koordinaten von jeweils -150 bis 150 in Zehnerschritten dar

• 

  Schritt 1: Rotation der a*/b*-Ebene um 16°

• 

  Schritt 2: Stauchung der f-Achse

• 

  Schritt 3: Radiale Kompression der e/f-Ebene

• 

  Vergrößerte Ansicht der a99/b99-Ebene

Anders als in den CIE94- und CIEDE2000-Formeln ist es für die Berechnung des Farbabstandes nicht erforderlich, den Bunttonwinkel zu ermitteln.

Zwischenberechnungen

Zuerst die Zwischenberechnungen, die zur Ermittlung des Farbabstandes notwendig sind:

a ^* und b ^* werden transformiert zu

Rotheitswerte (Rot-Grün-Achse)

$e= a^* \cdot \cos\left(16^\circ\right)+b^* \cdot \sin\left(16^\circ \right)$

Gelbheitswert f (Gelb-Blau-Achse)

$f = 0{,}7 \cdot \left(-a^* \cdot \sin \left(16^\circ\right)+b^* \cdot \cos\left(16^\circ\right)\right)$

Daraus errechnet sich dann Chromawert G (Buntheit):

$G=\sqrt {\left(e^2 + f^2 \right)}$

mit

$g=0{,}045 \cdot G$

und

$k= \frac{\ln \left( 1+g \right)}{g}$

Bunttonwerte

$a_{99}=k \cdot e$

$b_{99}=k \cdot f$

Tritt der Fall ein, dass a ^* = b ^* = 0, dann gilt a₉₉ = b₉₉ = 0

Farbabstandsformel

Der Farbabstand kann dann einfach mit folgender Formel analog zu ΔE ermittelt werden:

$\Delta E_{99} = \sqrt{ \left( \Delta L_{99} \right) ^2 + \left( \Delta a_{99} \right) ^2 + \left( \Delta b_{99} \right)^2}$

Weitere Berechnungen

Zur Berechnung kann auch ein vorläufiger Bunttonwinkel ermittelt werden:

$h_{99,ef} = \arctan \left( \frac{f}{e} \right)$ , Winkel im Bogenmaß

Buntheit (Chroma) und Bunttonwinkel (Hue)

Die Buntheit C₉₉ wird folgendermaßen berechnet:

$C_{99} = \frac{\ln \left( 1+ 0{,}045 \cdot G \right)}{0{,}045 \cdot k_{CH} \cdot k_E}$ , mit den variablen Parametern k_CH und k_E , Standardwerte k_CH = k_E = 1

Anmerkung: k_CH und k_E hängen von den jeweiligen Betrachtungsbedingungen ab, analog den Werten l und c in der CMC(l:c)-Farbabstandsformel. Andere Quellen (nicht DIN) geben für k_CH = 2,0 und für k_E = 0,5 an. In der DIN wird von einer Änderung der Faktoren abgeraten und für beide der Standardwert 1 empfohlen. Das Resultat bleibt durch die Multiplikation aber gleich.

Der Bunttonwinkel ergibt sich aus h_99,ef :

$h_{99} = h_{99,ef} \cdot \frac{180}{\pi}$ , Winkel in Grad

Bunttonwerte (alternativ)

Aus C₉₉ und h₉₉ lassen sich ebenfalls die Bunttonwerte berechnen:

$a_{99} = C_{99} \cdot \cos \left( h_{99} \right)$

$b_{99} = C_{99} \cdot \sin \left( h_{99} \right)$

Buntheitsdifferenz (Chroma-Differenz)

$\Delta C_{99} = C_{99,V} -C_{99,M} \frac{}{}$ , M = Musterfarbe, V = Vergleichsfarbe

Differenz des Bunttonwinkels

$\Delta h_{99} = \frac{a_{99,M} \cdot b_{99,V} - a_{99,V} \cdot b_{99,M}}{\sqrt{ 0,5 \cdot \left( C_{99,V} \cdot C_{99,M} + a_{99,V} \cdot a_{99,M} + b_{99,V} \cdot b_{99,M}\right)}}$ , M = Musterfarbe, V = Vergleichsfarbe

Farbabstand (alternative Berechnung)

Der Farbabstand lässt sich ebenfalls aus Buntheit und Bunttonwinkel berechnen:

$\Delta E_{99} =\sqrt{ \left( \Delta L_{99} \right) ^2 + \left( \Delta C_{99} \right) ^2 + \left( \Delta h_{99} \right)^2}$

Inverse Berechnungen

Folgende Formeln dienen der Ermittlung der entsprechenden Werte im CIELAB-Farbraum:

Zwischenwert für DIN99-Bunttonwinkel

Für alle Berechnungen in diesem Abschnitt gilt der Winkel im Bogenmaß.

$h_{99,ef} = \arctan \left( \frac{b_{99}}{a_{99}} \right)$ , für a₉₉ > 0 und b₉₉ ≥ 0

$h_{99,ef} = \frac{\pi}{2}$ , für a₉₉ = 0 und b₉₉ > 0

$h_{99,ef} = \pi + \arctan \left( \frac{b_{99}}{a_{99}} \right)$ , für a₉₉ < 0

$h_{99,ef} = \frac{3 \, \pi}{2}$ , für a₉₉ = 0 und b₉₉ < 0

$h_{99,ef} = 2\, \pi + \arctan \left( \frac{b_{99}}{a_{99}} \right)$ , für a₉₉ > 0 und b₉₉ ≤ 0

$h_{99,ef} = 0 \frac{ }{ }$ , für a₉₉ = 0 und b₉₉ = 0

Zwischenwert für DIN99-Buntheit

$G = \frac{\mathrm{exp} \left( 0{,}045 \cdot C_{99} \cdot k_{CH} \cdot k_E \right)-1}{0{,}045}$

Zwischenwert für DIN99-Rotheit

$e = G \cos \left( h_{99,ef}\right)$

Zwischenwert für DIN99-Gelbheit

$f = G \sin \left( h_{99,ef}\right)$

CIELAB-Rotheits- und Gelbheitsachsen

$a^{*} = e \cdot \cos (16^\circ) - \left( \frac{f}{0{,}7} \right) \sin (16^\circ)$

$b^{*} = e \cdot \sin (16^\circ) + \left( \frac{f}{0{,}7} \right) \cos (16^\circ)$

CIELAB-Helligkeit

$L^{*} = \frac{\mathrm{exp}\left( \frac{L_{99}\cdot k_E}{105{,}51} \right)- 1} {0{,}0158}$

Bei schon vorhandenen Werten h₉₉ und C₉₉

Wenn DIN99-Buntheitswert und Bunttonwinkel schon gegeben sind, dann berechne zuerst

$h_{99,ef} = h_{99} \cdot \frac{\pi}{180}$ , Winkel im Bogenmaß

und fahre mit der Berechnung ab dem Zwischenwert G für DIN99-Buntheit fort.

Qualität und Weiterentwicklung

Der DIN99-Farbraum nähert sehr gut die CIE94-Farbabstandsformel an und besitzt ähnliche qualitative Eigenschaften, auch vergleichbar mit CMC(l:c).^{[1] [2]} Ein großer Vorteil gegenüber CIE94 ist die Vertauschbarkeit von Muster- und Vergleichsprobe in der Berechnung, die dadurch ermöglicht wird, dass die Transformation vollständig und einfach umkehrbar ist. Der Unterschied zu CIELAB besteht in der verbesserten Übereinstimmung der Berechnungen mit wahrgenommenen Farbabständen.^[3] Die Modifikation der Helligkeitsachse und die stärkere Gewichtung der Farben nahe der Unbuntachse durch die Kompression stark gesättigter Farben erhöhen die Gleichabständigkeit wahrgenommener Farbabstände beträchtlich. Die Bewertungskategorien Helligkeits- und Bunttonachsen (Gelb-Blau und Rot-Grün) ändern sich im Vergleich zu CIELAB nicht. Die Berechnung des Farbabstandes als einfacher euklidischer Abstand ist ein großer Vorteil gegenüber CMC(l:c), CIE94 und CIEDE2000, deren Berechnung viel komplizierter ist. Nachträgliche Verbesserungen des DIN99-Farbraumes (DIN 6176:2001-03) stellen eine ähnliche Qualität her, wie sie mit CIE94 und CIEDE2000 erreicht wird. ^{[4] [5]}

Auch nach der Weiterentwicklung des DIN99-Farbraums bleibt ein Problem bestehen. Toleranzellipsen werden im blauen Bereich des DIN99-Farbraums immer noch als Ellipsen und nicht als Kreise abgebildet. Cui, Lou et al. modifizierten im Jahr 2001 die DIN99-Formeln, um dieses Problem zu Lösen. Dabei entstanden drei Farbraumvarianten: DIN99b, DIN99c und DIN99d. Als Basis zur Optimierung der DIN99-Formel und zur Beurteilung von Farbtoleranzen (der Toleranzellipsen nach MacAdams) dienten mehrere Farbtoleranz-Datensätze (VFD-P^[6], RIT-DuPont, Leeds^[7] und Witt^[8]), die zu einem Gesamtdatensatz zusammengeführt wurden. Qualitativ war die Beurteilung von Farbtoleranzen in der blauen Region des DIN99b-Farbraums schlechter als mit der CIEDE2000-Formel. Farbtoleranzen wurden in der blauen Region immer noch als Ellipsen abgebildet. Zur Lösung des Problems wurden die a*- und b*-Werte des CIELAB-Farbraums linearisiert und eine Blaukorrektur im CIELAB-Farbraum vorgenommen. Für die Blaukorrektur wurde der aus dem XYZ-Farbraum verwendete X-Wert einer Farbe zusätzlich mit einem Anteil des Z-Wertes gewichtet. Erst nach dieser Gewichtung findet die CIELAB-Berechnung statt, die die Basis für den DIN99-Farbraum darstellt. Diese Korrektur fließt sowohl in den DIN99c- als auch in den DIN99d-Farbraum ein. DIN99c ist im Gegensatz zu DIN99 nicht gedreht, also genauso orientiert wie der CIELAB-Farbraum. DIN99d ist jedoch gegenüber CIELAB um 50° gedreht. Bei Tests mit dem neuen Farbdatensatz stellen alle drei Varianten eine Verbesserung dar, jedoch bieten nur DIN99c und DIN99d wesentliche Verbesserungen gegenüber DIN99 in der besagten blauen Region. Farbtoleranz-Ellipsen werden auch im blauen Bereich sowohl in DIN99c als auch in DIN99d nahezu kreisförmig abgebildet. Diese Weiterentwicklung ermöglicht eine mit CIEDE2000 vergleichbare Qualität der Bestimmung von Farbtoleranzen und -abständen, bei geringerem Rechenaufwand.

Einzelnachweise

1. ↑ Dipl.-Ing. H. Büring: Eigenschaften des Farbenraumes nach DIN 6176 (DIN99-Formel) und seine Bedeutung für die industrielle Anwendung. http://kb-bmts.rz.tu-ilmenau.de/gcg/html/Vortr_02_pdf/GCG_%202002_%20Buering.pdf 2. Februar 2008.
2. ↑ Dr. L. Gall - Farbmetrik für Pigmentverarbeiter - DIN99 http://www.farbmetrik-gall.de/cielab/korrcielab/din99.html 2. Februar 2008
3. ↑ DIN 6174, Farbmetrische Bestimmung von Farbabständen bei Körperfarben nach der CIELAB-Formel
4. ↑ DIN 6176:2001-03, Farbmetrische Bestimmung von Farbabständen bei Körperfarben nach der DIN-99-Formel
5. ↑ Deutsche farbwissenschaftliche Gesellschaft e.V. : Pressemitteilung zum DIN 99 (DIN 6176) Farbenraum http://www.dfwg.de/doc/dfwg-homepage-417.htm 2. Februar 2008
6. ↑ M. R. Luo, B. Rigg, Chromaticity-discrimination ellipses for surface colours, Color Research and Application, 11:25-42, 1986
7. ↑ D. H. Kim, J. H. Nobbs, New weighting functions for the weighted CIELAB colour-difference formula, Proc Colour 97 Kyoto, 1:446-449, 1997
8. ↑ K. Witt, Geometric relations between scales of small colour-differences, Color Research and Application, 24:78-92, 1999