Dalitz-Plot

Das Dalitz-Diagramm ist ein Streudiagramm, das oft in der Teilchenphysik Anwendung findet. Dabei werden die Werte von kinematischen Variablen eines Streu- bzw. Zerfallsereignisses in einen Graph eingetragen. Die Punktdichte ist hierin ein Maß, wie häufig bestimmte (kinematisch unterschiedliche) Konfigurationen von (ansonsten ähnlichen) beispielsweise von Dreikörperzerfällen stattfinden.

Die Kinematik eines Dreikörperzerfalls kann mit nur zwei Variablen vollständig beschrieben werden. In herkömmlichen Dalitz-Diagrammen zeigen die Achsen das Quadrat der invarianten Masse von zwei Paaren der Zerfallsprodukte an. Zerfällt z. B. Teilchen A in drei Teilchen 1, 2 und 3, so könnten in einem Dalitz-Diagramm für diesen Zerfall 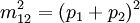$m^2_{12} = (p_1 + p_2)^2$ auf der x-Achse und 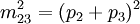$m^2_{23} = (p_2 + p_3)^2$ auf der y-Achse aufgetragen werden, wobei p_i die Viererimpulse sind und das Quadrat für das Minkowski-Produkt mit sich selbst steht.

Ist ein Zerfall ein reiner Dreikörperzerfall, bei dem das Mutterteilchen direkt in drei Teilchen zerfällt, so kann die Verteilung im Dalitz-Diagramm gleichförmig sein. Dreikörperzerfälle werden jedoch oft von Resonanzen dominiert, bei denen das Mutterteilchen zunächst in zwei Produktteilchen zerfällt, von denen eins sofort in die zwei Endprodukte weiterzerfällt. In diesem Fall zeigt das Dalitz-Diagramm eine ungleichmäßige Verteilung, mit einer höheren Punktdichte im Bereich der Masse des resonanten Zerfalls. Auf diese Weise ist das Dalitz-Diagramm ein hervorragendes Werkzeug, um die Dynamik von Dreikörperzerfällen zu studieren.

R. H. Dalitz führte diese Methode 1953 ein, um den Zerfall von K-Mesonen zu studieren, die damals noch "Tau-Mesonen" genannt wurden. Sie kann auch auf Vierkörperzerfälle erweitert werden. Eine spezifische Form von Vier-Teilchen Dalitz Diagrammen (fuer nicht-relativistische Kinematik), welche auf einem tetraedischen Koordinaten-System basieren, wurde erstmals entwickelt, um atomare Vier-Teilchen Fragmentierungs-Prozesse zu analysieren.

Literatur

• R. H. Dalitz, Phys. Rev. 94, 1046-1051 (1954)
• Dalitz Philosophical Magazine Bd.44, 1953, S.1068
• E. Fabri Nuovo Cimento Bd.11, 1954, S.479
• M. Schulz et al. J. Phys. B Bd. 40, S. 3091 2007
• M. Schulz, Phys. Rev. A Bd. 79, S. 042708 (2009)

Weblinks

• Bock in Briefbook Particle Detectors zu Dalitz Plots mit einem Beispiel