Adjunktion einer Derivation

Die semidirekte Summe ist eine mathematische Konstruktion aus der Theorie der Lie-Algebren.

Konstruktion

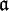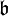Es seien ${\mathfrak a}$ und $\mathfrak b$ Lie-Algebren, 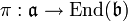$\pi: {\mathfrak a}\rightarrow {\rm End}({\mathfrak b})$ sei eine Darstellung, das heißt:

$π$ ist linear, und für alle 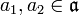$a_1,a_2\in {\mathfrak a}$ gilt $\pi([a_1,a_2]) \,=\, \pi(a_1)\pi(a_2) - \pi(a_2)\pi(a_1)$ .
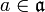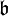$π(a)$ ist für jedes $a\in {\mathfrak a}$ eine Derivation auf ${\mathfrak b}$ .

Dann gibt es auf der direkten Summe 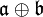${\mathfrak a}\oplus {\mathfrak b}$ der Vektorräume genau ein Produkt $[\cdot,\cdot]$ , so dass Folgendes gilt: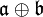

${\mathfrak a}\oplus {\mathfrak b}$ ist mit $[\cdot,\cdot]$ eine Lie-Algebra.
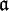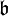Die Einschränkung Produktes auf ${\mathfrak a}$ und ${\mathfrak b}$ stimmt mit den dort gegebenen Produkten überein.
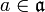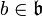Für alle $a\in {\mathfrak a}$ und $b\in {\mathfrak b}$ gilt $[a,b] \,=\, \pi(a)b$ .

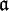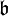Dabei werden ${\mathfrak a}$ und ${\mathfrak b}$ als Unterräume der direkten Summe aufgefasst.

Das Produkt auf 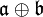${\mathfrak a}\oplus {\mathfrak b}$ lautet

$[(a_1,b_1)\, ,\,(a_2,b_2)] := ([a_1,a_2]\, ,\, [b_1,b_2] + \pi(a_1)b_2-\pi(a_2)b_1) ,\quad a_1,a_2\in {\mathfrak a},\, b_1,b_2\in {\mathfrak b}$ .

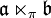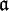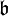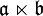Man rechnet nach, dass durch diese Definition eine Lie-Algebra gegeben ist. Diese wird mit ${\mathfrak a}\ltimes_{\pi} {\mathfrak b}$ bezeichnet und heißt die semidirekte Summe oder auch das semidirekte Produkt aus ${\mathfrak a}$ und $\mathfrak b$ . Wenn es bezüglich der Darstellung $π$ keine Missverständnisse geben kann, so lässt man sie weg und schreibt einfach ${\mathfrak a}\ltimes {\mathfrak b}$ .

Bemerkungen

In obiger Konstruktion ist 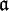${\mathfrak a}$ eine Lie-Unteralgebra der semidirekten Summe und 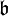${\mathfrak b}$ sogar ein Ideal, das heißt $[{\mathfrak a}\ltimes {\mathfrak b},{\mathfrak b}] \subset {\mathfrak b}$ .
Ist $π = 0$ , so liegt die direkte Summe der Lie-Algebren vor.
Seien 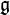${\mathfrak g}$ eine Lie-Algebra über dem Körper $K$ und $d$ eine Derivation auf 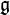${\mathfrak g}$ . Dann ist 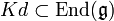$Kd \subset {\rm End}({\mathfrak g})$ eine Darstellung, und man kann 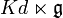$Kd \ltimes {\mathfrak g}$ bilden. Dies nennt man auch die Adjunktion der Derivation $d$ .