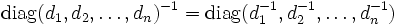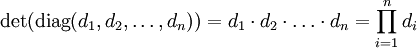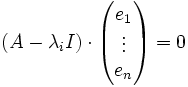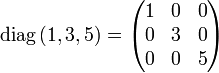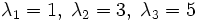- Diagonalisierbar
-
Als Diagonalmatrix bezeichnet man im mathematischen Teilgebiet der linearen Algebra eine quadratische Matrix, bei der alle Elemente außerhalb der Hauptdiagonale Null sind. Diagonalmatrizen sind deshalb allein durch die Angabe ihrer Hauptdiagonale bestimmt und man schreibt häufig
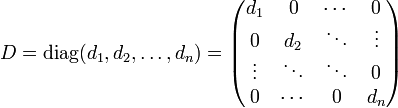 .
.
Inhaltsverzeichnis
Rechenoperationen
Matrixaddition, Skalarmultiplikation und Matrixmultiplikation
Die Matrixaddition, Skalarmultiplikation und Matrixmultiplikation gestalten sich bei Diagonalmatrizen sehr einfach:
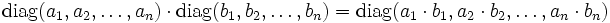
Multiplikation einer Matrix A von links mit einer Diagonalmatrix entspricht der Multiplikation der Zeilen von A mit den Diagonaleinträgen. Die entsprechende Multiplikation von Rechts entspricht der Multiplikation der Spalten von A mit den Diagonaleinträgen.
Berechnung der Inversen
Eine Diagonalmatrix ist genau dann invertierbar, wenn keiner der Einträge auf der Hauptdiagonale 0 ist. Die inverse Matrix berechnet sich dann wie folgt:
Eigenschaften von Diagonalmatrizen
- Die jeweiligen Diagonalmatrizen bilden einen kommutativen Unterring des Rings der quadratischen
 -Matrizen.
-Matrizen. - Die Eigenwerte einer Diagonalmatrix sind die Einträge auf der Hauptdiagonale mit den kanonischen Einheitsvektoren als Eigenvektoren.
- Die Determinante einer Diagonalmatrix ist das Produkt der Einträge auf der Hauptdiagonalen:
Diagonalisierbarkeit
Eine beliebige quadratische Matrix A heißt diagonalisierbar, wenn es eine Diagonalmatrix D gibt, zu der sie ähnlich ist.
Für eine lineare Abbildung
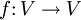 (Vektorraum-Endomorphismus) bedeutet dies, dass eine Basis B existiert, bei der die Darstellungsmatrix
(Vektorraum-Endomorphismus) bedeutet dies, dass eine Basis B existiert, bei der die Darstellungsmatrix 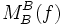 eine Diagonalmatrix ist.
eine Diagonalmatrix ist.Alternativ lässt sich auch definieren: eine quadratische
 Matrix A ist genau dann diagonalisierbar, wenn es n linear unabhängige Eigenvektoren von A gibt.
Matrix A ist genau dann diagonalisierbar, wenn es n linear unabhängige Eigenvektoren von A gibt.Eigenschaften einer diagonalisierbaren Matrix
Ist eine Matrix diagonalisierbar, so ist die geometrische Vielfachheit ihrer Eigenwerte gleich der jeweiligen algebraischen Vielfachheit. Das bedeutet, die Dimension der einzelnen Eigenräume stimmt jeweils mit der algebraischen Vielfachheit der entsprechenden Eigenwerte im charakteristischen Polynom der Matrix überein.
Diagonalisierung
Ist eine Matrix A diagonalisierbar, existiert eine Diagonalmatrix DA für die die Ähnlichkeitsbedingung erfüllt ist:
- DA = S − 1AS
Zur Diagonalisierung dieser Matrix berechnet man die Diagonalmatrix DA und die zugehörige Basis. Dies geschieht in drei Schritten:
- Es werden die Eigenwerte λi der Matrix A bestimmt.
- Es werden die Eigenräume
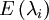 zu allen Eigenwerten λi berechnet, also folgendes Gleichungssystem gelöst:
zu allen Eigenwerten λi berechnet, also folgendes Gleichungssystem gelöst:
- Nun ist die Diagonalform DA der Matrix A bezüglich der Basis B:
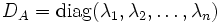
- S = {E(λ1),...,E(λn)}
Simultane Diagonalisierung
Gelegentlich will man auch zwei unterschiedliche Matrizen A,B mit derselben Transformation S diagonalisieren. Falls das gelingt, gilt S − 1AS = D1 und S − 1BS = D2 und da D1 und D2 Diagonalmatrizen sind,
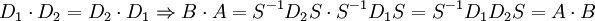 .
.
Also müssen die Endomorphismen miteinander kommutieren. In der Tat gilt auch die Umkehrung: kommutieren zwei diagonalisierbare Endomorphismen, so können sie simultan diagonalisiert werden. In der Quantenmechanik gibt es für zwei solche Operatoren dann eine Basis aus gemeinsamen Eigenzuständen.
Beispiel
Die Diagonalmatrix
besitzt die Eigenwerte
mit zugehörigen Eigenräumen / Eigenvektoren
![E_1=[\begin{pmatrix}
1 \\
0 \\
0
\end{pmatrix}],\quad
E_2=[\begin{pmatrix}
0 \\
1 \\
0
\end{pmatrix}],\quad
E_3=[\begin{pmatrix}
0 \\
0 \\
1
\end{pmatrix}]](/pictures/dewiki/102/f48e91622091c8b607e96a67506db0a9.png) .
.
Spezielle Diagonalmatrizen
- Die Einheitsmatrix ist ein Spezialfall einer Diagonalmatrix, bei der alle Elemente der Hauptdiagonale den Wert 1 haben.
- Die quadratische Nullmatrix ist ein Spezialfall einer Diagonalmatrix, bei der alle Elemente der Hauptdiagonale den Wert 0 haben.
Siehe auch
Wikimedia Foundation.