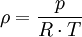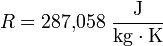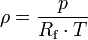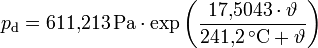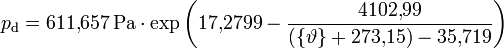Dichte der Luft

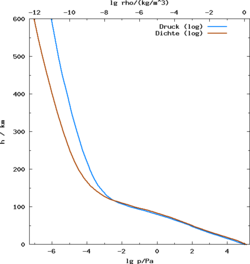Abbildung 3: Durchschnittlicher Luftdruck und Luftdichte in Abhängigkeit von der Höhe.

Die Luftdichte ρ (auch: Dichte von Luft oder Dichte der Luft) gibt an, wie viel Masse an Luft (in kg) in einem bestimmten Volumen (in m³) enthalten ist. Auf Meeresspiegelhöhe ist die Luft mit rund 1,2041 kg/m³ bei 20 °C durch die darüber lastende Luftmasse stärker zusammengedrückt als in größerer Höhe: die Luft ist also sehr dicht.

Sie hat am Boden immer höchste Dichte und höchsten Luftdruck - und außer bei Inversionen auch die höchste Temperatur. In größeren Höhen wird die Luft immer dünner. Wäre die Temperatur in allen Höhen gleich, so würden Luftdruck und Luftdichte auch gemeinsam mit zunehmender Höhe nach dem Gasgesetz abnehmen (siehe Barometrische Höhenformel). Die Temperatur in verschiedenen Höhen variiert jedoch stark.

Die theoretische Abnahme von Druck und Dichte der Luft pro 5000 Meter - wobei sie auf die Hälfte fallen müsste - stimmt nicht genau; die Abweichungen sind aber gering.

90 % der Atmosphäre liegen unter 20 km Höhe.

75 % der Atmosphäre liegen unter 10 km Höhe.

50 % der Atmosphäre liegen unter 5 km Höhe.

Die Luftdichte ρ ist:

$\rho = \frac{p}{R \cdot T}$

in kg/m³; Luftdruck = p, Gaskonstante R, Temperatur in Kelvin = T

Die individuelle Gaskonstante R für trockene Luft ist:

$R = 287{,}058\ \mathrm{\frac{J}{kg \cdot K}}$

mit Energie Joule (J) = Newton · Meter = N m; {T in Kelvin} = {Temperatur in °C} + 273,15.

Atmosphärischer Luftdruck p₀ = 101325 Pa = 1013,25 mbar = 1013,25 hPa und R = 287,058 J/kg · K.

Bei T₀ = 273,15 K (0 °C) (Normalbedingungen) ist die Luftdichte:

ρ₀ = 101325 / (287,05 · 273,15) = 1,293 kg/m³.

Bei T₂₅ = 298,15 K (25 °C) (Standardbedingungen) ist die Luftdichte:

ρ₂₅ = 101325 / (287,058 · 298,15) = 1,184 kg/m³.

Weiterhin ist üblich T₂₀ = 293,15 K ⇔ 20 °C und dabei ist die Luftdichte ρ = 1,204 kg/m³.

Wie man erkennt, sind diese Größen stark temperaturabhängig.

Exakte Dichtebestimmung der Luft

Eine exakte Dichtebestimmung der Luft erfordert eine Berücksichtigung der Luftfeuchte, da diese die Gaskonstante der Luft verändert. Nachdem die Gaskonstante angepasst wurde, wird die Gleichung

$\rho = \frac{p}{R_\mathrm{f} \cdot T}$

weiter verwendet werden. Die Gaskonstante der feuchten Luft berechnet sich durch:

$R_\mathrm{f} = \frac{R_\mathrm{l}}{1 - ( \varphi \cdot p_\mathrm{d}/p)\cdot (1 - R_\mathrm{l}/R_\mathrm{d})}$,

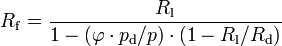wobei

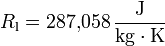$R_\mathrm{l} = 287{,}058\, \frac{\mathrm{J}}{\mathrm{kg} \cdot \mathrm{K}}$ die Gaskonstante der trockenen Luft,

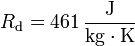$R_\mathrm{d} = 461\, \frac{\mathrm{J}}{\mathrm{kg} \cdot \mathrm{K}}$ die Gaskonstante von Wasserdampf,

$\varphi$ die relative Luftfeuchtigkeit (z. B. 0,76 entsprechend 76 %) und

p der Umgebungsdruck in Pascal ist.

p_d ist der Sättigungsdampfdruck von Wasser in Luft und errechnet sich empirisch mit Hilfe der Magnus-Formel

(Näheres hierzu siehe Sättigungsdampfdruck, man beachte die Nebenbedingungen!):

$p_\mathrm{d} = 611{,}213\,\mathrm{Pa} \cdot \exp \left( \frac{17{,}5043 \cdot \vartheta}{241{,}2\,^{\circ}\mathrm{C} + \vartheta} \right)$

wobei für 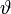$\vartheta$ die Umgebungstemperatur in °C zwischen -30°C und +70°C eingesetzt wird. Die Gleichung liefert den Dampfdruck in Pascal. Alternativ kann auch die Formel

$p_\mathrm{d} = 611{,}657\,\mathrm{Pa} \cdot \exp \left( 17{,}2799 - \frac{4102{,}99}{(\{\vartheta\} + 273{,}15) - 35{,}719} \right)$

verwendet werden; besonders genaue Werte liefert ein Tafelwerk (Dampftafel).

Um den Messfehler zu minimieren, empfiehlt sich zur Bestimmung der Luftfeuchte ein Aspirationspsychrometer und zur Bestimmung des Umgebungsdrucks ein Quecksilberbarometer, wobei der Barometerstand noch um Kapillarität, Kuppenhöhe des Quecksilberpegels, temperaturabhängige Dichte des Quecksilbers und lokale Erdschwerebeschleunigung korrigiert werden muss.

Tabellen

Die Wirkung der Temperatur

Schallkennimpedanz, Luftdichte und Schallgeschwindigkeit in Abhängigkeit von der Lufttemperatur

Temperatur ϑ in °C	Schallgeschwindigkeit c in m/s	Dichte ρ in kg/m³	Kennimpedanz ZF in Ns/m³
− 25	316,0	1,423	449,7
− 20	319,1	1,395	445,1
− 15	322,3	1,368	440,9
− 10	325,4	1,341	436,5
− 5	328,5	1,316	432,4
0	331,5	1,293	428,3
+ 5	334,5	1,269	424,5
+ 10	337,5	1,247	420,7
+ 15	340,5	1,225	417,0
+ 20	343,4	1,204	413,5
+ 25	346,3	1,184	410,0
+ 30	349,2	1,164	406,5
+ 35	352,1	1,146	403,5

p = Schalldruck in Pa = Pascal = N/m² (p = F/A)

A = Fläche in m²

F = Kraft in N = Newton = kg·m/s²

ρ = rho = Luftdichte in kg/m³

c = Schallgeschwindigkeit in m/s

Z = Schallkennimpedanz in N · s/m³

In der Meteorologie benutzt man häufig auch den reziproken Wert der Dichte und bezeichnet die Größe als spezifisches Volumen α.

$\alpha = \frac{1} {\rho}$.

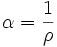Weblinks

• Kategorie:Meteorologie
• Kategorie:Flugmeteorologie