Dividierbar

In der Mathematik heißt eine Gruppe G teilbar oder dividierbar, falls es möglich ist, aus jedem Element n-te Wurzeln zu ziehen. Dieses Wurzelelement ist im Allgemeinen nicht eindeutig.

In Formeln bedeutet dies: $(\forall x \in G) (\forall n \in \mathbb{N}) (\exists y \in G) y^n=x$

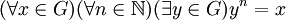
Dies ist äquivalent zu der Bedingung, dass Potenzieren mit natürlichen Zahlen surjektiv ist.

Der Begriff dividierbar erklärt sich dadurch, dass das Potenzieren im Fall additiv geschriebener abelscher Gruppen ein Multiplizieren mit n ist und die Umkehrung folglich eine Division.

Beispiele

• Das wichtigste Beispiel ist die additive Gruppe der rationalen Zahlen 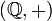$(\mathbb{Q},+)$. Hier ist das gesuchte Element sogar eindeutig.
• Die additive Gruppe jedes Vektorraums über den rationalen Zahlen ist dividierbar, insbesondere gilt dies für $(\mathbb{Q}^n,+), (\mathbb{R},+), (\mathbb{C},+), (\mathbb{R}^n,+), (\mathbb{C}^n,+)$
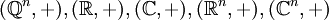
• Ein Gruppenhomomorphismus bildet dividierbare Gruppen auf dividierbare Gruppen ab, insbesondere sind Quotienten dividierbarer Gruppen dividierbar: z. B. $(\mathbb{Q}/\mathbb{Z},+), (\mathbb{R}/\mathbb{Z},+)$
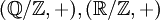
• Endliche Gruppen sind nicht dividierbar, denn für n=|G| ist das Potenzieren mit n nicht surjektiv (außer G ist einelementig)
• Für jede Primzahl p ist die Prüfer-Gruppe 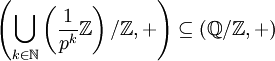$\left( \bigcup_{k \in \mathbb{N}}\left(\frac{1}{p^k}\mathbb{Z} \right)/\mathbb{Z} ,+\right) \subseteq (\mathbb{Q}/\mathbb{Z},+)$ dividierbar.
• die Einheitengruppe der Quaternionen 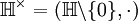$\mathbb{H}^\times = \left( \mathbb{H} \backslash \{0\} , \cdot \right)$ ist ein nichtkommutatives Beispiel einer dividierbaren Gruppe.
• ein weiteres nichtkommutatives Beispiel ist die dreidimensionale Spezielle orthogonale Gruppe 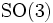$\operatorname{SO}(3)$, die aus den Rotationen im $\mathbb{R}^3$ besteht.

Dividierbare Abelsche Gruppen

Dividierbare abelsche Gruppen erfüllen folgende universelle Eigenschaft: (G,+) ist dividierbar genau dann, wenn für jede beliebige Untergruppe B einer abelschen Gruppe A gilt, dass sich jeder auf B definierte Homomorphismus nach G auf ganz A fortsetzen lässt, in Formeln: $(\forall (A,+) \textrm{ abelsch }) (\forall B \leq A) (\forall f \in \textrm{Hom}(B,G))(\exists g \in \textrm{Hom}(A,G)) g|_B = f$

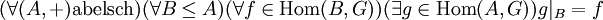
In der Sprache der Kategorientheorie lässt sich dies ausdrücken als: In der Kategorie der abelschen Gruppen sind die injektiven Objekte genau die dividierbaren abelschen Gruppen.

Struktursatz Dividierbarer Abelscher Gruppen

Jede dividierbare abelsche Gruppe ist isomorph zu einer direkten Summe von $\mathbb{Q}$-Vektorräumen und Prüfer-Gruppen.