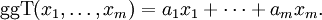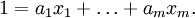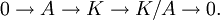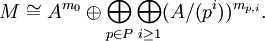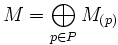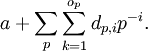- Elementarteilersatz
-
In der Algebra bezeichnet man Integritätsbereiche als Hauptidealringe oder Hauptidealbereiche, wenn jedes Ideal ein Hauptideal ist. Die wichtigsten Beispiele für Hauptidealringe sind der Ring der ganzen Zahlen sowie Polynomringe in einer Unbestimmten über einem Körper. Der Begriff des Hauptidealrings erlaubt es, Aussagen über diese beiden Spezialfälle einheitlich zu formulieren. Beispiele für Anwendungen der allgemeinen Theorie sind die Jordansche Normalform, die Partialbruchzerlegung oder die Strukturtheorie endlich erzeugter abelscher Gruppen.
Inhaltsverzeichnis
Definition
Ein Integritätsbereich A (d. h. ein nullteilerfreier kommutativer Ring mit
 ) heißt Hauptidealring, wenn jedes Ideal
) heißt Hauptidealring, wenn jedes Ideal 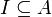 ein Hauptideal ist, d.h. es gibt ein
ein Hauptideal ist, d.h. es gibt ein  , so dass
, so dass 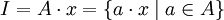 .
.Im Folgenden sei A ein Hauptidealring und K sein Quotientenkörper. Außerdem sei
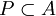 eine Menge, die für jedes irreduzible
eine Menge, die für jedes irreduzible  genau ein zu p assoziiertes Element enthält. Im Fall
genau ein zu p assoziiertes Element enthält. Im Fall 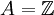 ist die Menge der (positiven) Primzahlen ein solches P, im Fall A = k[T] für einen Körper k die Menge der irreduziblen Polynome mit Leitkoeffizient 1.
ist die Menge der (positiven) Primzahlen ein solches P, im Fall A = k[T] für einen Körper k die Menge der irreduziblen Polynome mit Leitkoeffizient 1.Allgemeine Implikationen
Die folgenden Ringe sind Hauptidealringe:
- Körper
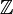 (der Ring der ganzen Zahlen)
(der Ring der ganzen Zahlen)![\Z[i]](/pictures/dewiki/56/89d7b73007774eb3de166a86b7686ac6.png) (der Ring der ganzen gaußschen Zahlen), der Ring der Eisenstein-Zahlen
(der Ring der ganzen gaußschen Zahlen), der Ring der Eisenstein-Zahlen- Polynomringe k[T] in einer Unbestimmten über einem Körper k
- formale Potenzreihenringe k[[T]] in einer Unbestimmten über einem Körper k
- diskrete Bewertungsringe
- euklidische Ringe (diese Klasse umfasst zwar alle vorstehenden Beispiele, aber nicht jeder Hauptidealring ist euklidisch)
Hauptidealringe gehören zu den folgenden allgemeineren Klassen von Ringen:
- faktorielle Ringe.[1] Insbesondere gelten:
-
- Ein Element
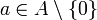 ist genau dann prim, wenn es irreduzibel ist.
ist genau dann prim, wenn es irreduzibel ist. - Jedes Element ungleich null des Quotientenkörpers von A lässt sich auf eindeutige Weise in der Form
-
- mit ganzen Zahlen ep und einer Einheit
 schreiben.
schreiben.
- Das Lemma von Gauß: Jedes irreduzible Element in A[X] ist entweder ein irreduzibles Element von A (aufgefasst als konstantes Polynom) oder ein in K[X] irreduzibles Polynom, dessen Koeffizienten teilerfremd sind.[2]
- Ein Element
- Dedekind-Ringe (siehe auch unten)
Ist A ein Hauptidealring, so ist auch jede Lokalisierung von A ein Hauptidealring.
Teilbarkeit
- Der (bis auf Assoziiertheit eindeutige) größte gemeinsame Teiler von Elementen
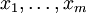 ist der (bis auf Assoziiertheit eindeutige) Erzeuger des Ideals
ist der (bis auf Assoziiertheit eindeutige) Erzeuger des Ideals  . Insbesondere gilt das Lemma von Bézout: Es existieren
. Insbesondere gilt das Lemma von Bézout: Es existieren 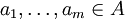 mit
mit
-
- Spezialfall:
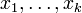 sind genau dann teilerfremd, wenn es
sind genau dann teilerfremd, wenn es  gibt mit
gibt mit
- Das kleinste gemeinsame Vielfache von
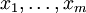 ist der Erzeuger des Ideals
ist der Erzeuger des Ideals 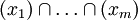 .
. - Chinesischer Restsatz: Sind
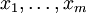 paarweise teilerfremd, so ist der kanonische Ringhomomorphismus
paarweise teilerfremd, so ist der kanonische Ringhomomorphismus
-
- ein Isomorphismus.[3]
- Eine Verschärfung des chinesischen Restsatzes ist der Approximationssatz: Gegeben seien
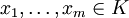 , paarweise verschiedene
, paarweise verschiedene 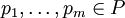 sowie Zahlen
sowie Zahlen 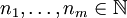 . Dann gibt es ein
. Dann gibt es ein  , das xi bezüglich pi in ni-ter Ordnung approximiert und ansonsten regulär ist, d.h.
, das xi bezüglich pi in ni-ter Ordnung approximiert und ansonsten regulär ist, d.h.
-
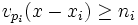 für
für 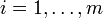
- und
 für
für 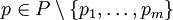 .
.
- Dabei bezeichnet
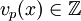 den Exponenten von p in der Primfaktorzerlegung von x.[4]
den Exponenten von p in der Primfaktorzerlegung von x.[4]
- Für
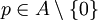 sind äquivalent:
sind äquivalent:
- p ist irreduzibel
- p ist ein Primelement
- (p) ist ein Primideal
- (p) ist ein maximales Ideal
- Das Nullideal ist ebenfalls ein Primideal, jedoch nur dann maximal, wenn A ein Körper ist.
Hauptidealringe als Dedekind-Ringe
- Hauptartikel: Dedekind-Ring
Viele in algebraischer Zahlentheorie und algebraischer Geometrie natürlich auftretende Ringe sind keine Hauptidealringe, sondern gehören einer etwas allgemeineren Klasse von Ringen an, den Dedekind-Ringen. Sie sind die lokalisierte Version der Hauptidealringe, Ideale sind nicht mehr global, sondern nur noch lokal von einem Element erzeugt:
- Ist A ein noetherscher Integritätsbereich, für den der lokale Ring
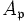 für jedes Primideal
für jedes Primideal 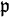 ein Hauptidealring ist, so heißt A Dedekind-Ring.[5]
ein Hauptidealring ist, so heißt A Dedekind-Ring.[5]
Die folgenden Eigenschaften gelten für Hauptidealringe, aber auch allgemeiner für Dedekind-Ringe:
- Sie sind entweder Körper oder eindimensional, d.h. jedes Primideal ungleich (0) ist maximal.
- Sie sind ganzabgeschlossen in ihrem Quotientenkörper.
- Sie sind regulär.
- Ihre lokalen Ringe sind entweder Körper oder diskrete Bewertungsringe.
- der oben genannte Approximationssatz
Ist ein Dedekind-Ring faktoriell oder semilokal, so ist er ein Hauptidealring.
Moduln über Hauptidealringen
Allgemeines
- Untermoduln freier Moduln sind frei.[6]
- Ist M ein endlich erzeugter Modul mit Torsionsuntermodul T, so gibt es einen freien Untermodul
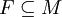 , so dass
, so dass 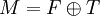 . Torsionsfreie, endlich erzeugte Moduln sind frei.[7]
. Torsionsfreie, endlich erzeugte Moduln sind frei.[7] - Projektive Moduln sind frei.[8]
- Ein Modul ist injektiv genau dann, wenn er dividierbar ist. Quotienten injektiver Moduln sind injektiv, jeder Modul hat eine injektive Auflösung der Länge 1. Eine explizite injektive Auflösung von A ist[9]
Endlich erzeugte Moduln: Elementarteilersatz
Der Elementarteilersatz beschreibt die Struktur einer Zerlegung eines endlich erzeugten Moduls in unzerlegbare Moduln. (Ein Modul M heißt unzerlegbar, wenn es keine Moduln
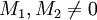 gibt mit
gibt mit 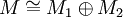 .)
.)Es sei P wie oben ein Vetretersystem der irreduziblen Elemente (bis auf Assoziiertheit). Zu jedem endlich erzeugten Modul M gibt es eindeutig bestimmte nichtnegative ganze Zahlen m0 und mp,i für
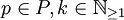 , von denen fast alle null sind, so dass
, von denen fast alle null sind, so dassDie Zahlen m0,mp,i sind durch M eindeutig festgelegt, und die einzelnen Faktoren A bzw. A / (pk) sind unzerlegbar. Die Ideale (pi), für die
 gilt, heißen Elementarteiler von M.[10]
gilt, heißen Elementarteiler von M.[10]Endlich erzeugte Moduln: Invariante Faktoren
Zu jedem endlich erzeugten Modul M gibt es eine endliche Folge
 von Elementen von A, die nicht notwendigerweise von null verschieden sind, so dass
von Elementen von A, die nicht notwendigerweise von null verschieden sind, so dass für
für 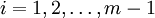
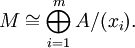
Die Ideale (xi) sind durch M eindeutig bestimmt und heißen die invarianten Faktoren von M. Die Elemente xi sind folglich bis auf Assoziiertheit eindeutig bestimmt.[11]
Zu dieser Aussage über Moduln gibt es zwei konkurrierende Sichtweisen:
- Zu einem Modul M kann man Erzeuger
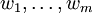 wählen und den Kern
wählen und den Kern 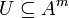 des zugehörigen Homomorphismus
des zugehörigen Homomorphismus 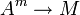 betrachten.
betrachten. - Zu einem Untermodul
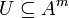 kann man Erzeuger
kann man Erzeuger 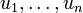 wählen und die
wählen und die 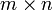 -Matrix X mit Einträgen in A betrachten, die den Homomorphismus
-Matrix X mit Einträgen in A betrachten, die den Homomorphismus 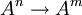 mit Bild U beschreibt.
mit Bild U beschreibt.
Umgekehrt ist das Bild einer
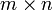 -Matrix mit Einträgen in A ein Untermodul
-Matrix mit Einträgen in A ein Untermodul 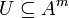 , und der Quotientenmodul M = Am / U (der Kokern des durch X gegebenen Homomorphismus
, und der Quotientenmodul M = Am / U (der Kokern des durch X gegebenen Homomorphismus 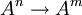 ) ist ein endlich erzeugter A-Modul.
) ist ein endlich erzeugter A-Modul.Für Untermoduln freier Moduln lautet die Aussage:
- Ist F ein freier A-Modul und U ein (ebenfalls freier) Untermodul von F vom Rang r, so gibt es n Elemente
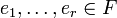 , die Teil einer Basis von F sind, sowie Elemente
, die Teil einer Basis von F sind, sowie Elemente 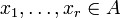 mit
mit 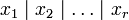 , so dass
, so dass 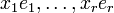 eine Basis von U ist. Der von den ek aufgespannte Teil
eine Basis von U ist. Der von den ek aufgespannte Teil 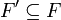 lässt sich invariant als das Urbild des Torsionsuntermoduls von F / U beschreiben. Die Ideale (xk) sind die Invarianten (wie oben) des Moduls F' / U, evtl. ergänzt um
lässt sich invariant als das Urbild des Torsionsuntermoduls von F / U beschreiben. Die Ideale (xk) sind die Invarianten (wie oben) des Moduls F' / U, evtl. ergänzt um 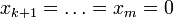 .[12]
.[12]
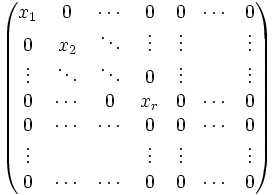
Für Matrizen (Smith-Normalform):
- Ist X eine
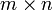 -Matrix mit Einträgen vom Rang r mit Einträgen in A, so gibt es invertierbare Matrizen
-Matrix mit Einträgen vom Rang r mit Einträgen in A, so gibt es invertierbare Matrizen  , so dass PXQ folgende Gestalt hat:
, so dass PXQ folgende Gestalt hat:
-
- Dabei sind
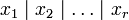 wieder die Invarianten wie oben.[13]
wieder die Invarianten wie oben.[13]
Torsionsmoduln
Es sei M ein (nicht notwendigerweise endlich erzeugter) Torsionsmodul über A, d.h. für jedes
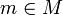 existiert ein
existiert ein 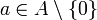 mit am = 0. Wieder sei
mit am = 0. Wieder sei 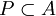 ein Vertretersystem der irreduziblen Elemente. Dann gilt:[14] M ist die direkte Summe der p-primären Untermoduln M(p), d.h.
ein Vertretersystem der irreduziblen Elemente. Dann gilt:[14] M ist die direkte Summe der p-primären Untermoduln M(p), d.h.mit
Als Korollar ergibt sich, dass M genau dann halbeinfach ist, wenn
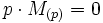 für alle
für alle  .[15]
.[15]Anwendungsbeispiele:
- Ist
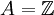 und
und  , so lautet die Aussage: Jede rationale Zahl besitzt eine eindeutige Darstellung
, so lautet die Aussage: Jede rationale Zahl besitzt eine eindeutige Darstellung
-
- mit
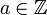 ,
, 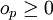 (und fast alle op = 0) sowie
(und fast alle op = 0) sowie 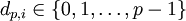 und
und 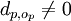 .[16]
.[16]
- Ist A = k[T] (k ein Körper) und M = K / A = k(T) / k[T], so entspricht M(p) den rationalen Funktionen, deren Nenner eine Potenz von p ist. Der Satz liefert also den ersten Schritt der Partialbruchzerlegung, d.h. der eindeutigen Darstellung einer rationalen Funktion als
-
- Dabei durchläuft p die irreduziblen normierten Polynome in k[T], die weiteren Komponenten sind der reguläre Anteil
![a\in k[T]](/pictures/dewiki/52/485cd271b192bbbf9203747c621b8883.png) , die Ordnungen
, die Ordnungen 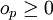 (fast alle op = 0) und geeignete Polynome dp,i für
(fast alle op = 0) und geeignete Polynome dp,i für  mit deg(dp,i) < deg(p). Ist insbesondere p linear, so sind die dp,i Konstanten.[17]
mit deg(dp,i) < deg(p). Ist insbesondere p linear, so sind die dp,i Konstanten.[17]
- Ist A = k[T] und M ein endlichdimensionaler k-Vektorraum zusammen mit einem Endomorphismus f (mit der A-Modulstruktur Tv = f(v)), so ist die obige Zerlegung die Aufspaltung in die Haupträume. Das Korollar besagt in diesem Fall, dass f genau dann halbeinfach ist, wenn das Minimalpolynom von f keine mehrfachen Faktoren enthält.[18]
Verwandte Begriffe
- Wird nur gefordert, dass jedes Ideal endlich erzeugt ist, gelangt man zum Begriff des noetherschen Rings.
- Manchmal werden auch nicht nullteilerfreie Ringe in der Definition des Begriffes "Hauptidealring" erlaubt, es wird also nur gefordert, dass jedes Ideal ein Hauptideal ist und
 .[19] Im Englischen kann sprachlich zwischen principal ideal ring und principal ideal domain (domain = Integritätsbereich) unterschieden werden, im Deutschen ist das unüblich.
.[19] Im Englischen kann sprachlich zwischen principal ideal ring und principal ideal domain (domain = Integritätsbereich) unterschieden werden, im Deutschen ist das unüblich.
Literatur
- Lang, S., Algebra, Springer 2002
- Bourbaki, N., Elements of Mathematics, Algebra II, Chapters 4-7, Springer 1990
- Bourbaki, N., Eléments de Mathématique, Algèbre, Chapitre 10, Algèbre homologique, Springer 2007
- Bourbaki, N., Elements of Mathematics, Commutative Algebra, Chapters 1-7, Springer 1989
Einzelnachweise
- ↑ Lang, Theorem II.5.2, S. 112
- ↑ Lang, Theorem IV.2.3, S. 182
- ↑ Lang, Corollary II.2.2, S. 95
- ↑ Bourbaki, Commutative Algebra, Ch. VII, §2.4, Proposition 2
- ↑ Bourbaki, Commutative Algebra, Ch. VII, §2
- ↑ Bourbaki, Algebra, Ch. VII, § 3, Corollary 2; Lang, Theorem III.7.1
- ↑ Bourbaki, Algebra, Ch. VII, § 4, No. 4, Corollary 1 und 2; Lang, Theorem III.7.3
- ↑ Bourbaki, Algebra, Ch. VII, § 3, Corollary 3
- ↑ Bourbaki, Algèbre, Ch. X, § 1, No. 7, Corollaire 2
- ↑ Bourbaki, Algebra, Ch. VII, § 4, No. 8, Proposition 9; Lang, Theorem III.7.5
- ↑ Bourbaki, Algebra, Ch. VII, § 4, No. 4, Theorem 2; Lang, Theorem III.7.7
- ↑ Bourbaki, Algebra, Ch. VII, § 4, No. 3, Theorem 1; Lang, Theorem III.7.8
- ↑ Bourbaki, Algebra, Ch. VII, § 4, No. 6, Corollary 1; Lang, Theorem III.7.9
- ↑ Bourbaki, Algebra, Ch. VII, § 2, No. 2, Theorem 1
- ↑ Bourbaki, Algebra, Ch. VII, § 2, No. 2, Corollary 4
- ↑ Bourbaki, Algebra, Ch. VII, § 2, No. 3, I
- ↑ Bourbaki, Algebra, Ch. VII, § 2, No. 3, II
- ↑ Bourbaki, Algebra, Ch. VII, § 5, No. 8, Proposition 14
- ↑ Lang, II, §1, S. 86
Wikimedia Foundation.