Divisions-Rest-Methode

Die Divisions-Rest-Methode (siehe auch Modulo) liefert eine Hash-Funktion.

Die Funktion lautet: $h(k) = k \mod m$

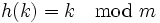
m ist die Größe der Hashtabelle.

Eigenschaften

1. Die Hash-Funktion kann sehr schnell berechnet werden
2. Die Wahl der Tabellengröße m beeinflusst die Kollisionswahrscheinlichkeit der Funktionswerte von h.

Für die meisten Eingabedaten ist z.B. die Wahl einer Zweierpotenz für m, also m = 2ⁱ, ungeeignet, da dies der Extraktion der i-niedrigstwertigen Bits von k entspricht, so dass alle höherwertigen Bits bei der Hash-Berechnung ignoriert werden.

Für praxisrelevante Anwendungen liefert die Wahl einer Primzahl für m, welche nicht zu nah an einer Zweierpotenz liegt, eine geringe Anzahl von zu erwartenden Kollisionen bei vielen Eingabedatenverteilungen^[1].

Hashing von Strings

Strings können mit der Divisionsmethode gehasht werden, indem die Zeichenketten in ganze Zahlen zur Basis b umgewandelt werden, wobei b die Zeichensatzgröße bezeichnet.

Um Integer-Überläufe zu vermeiden, kann für die Berechnung des Hashwertes bei Schlüsseln das Horner-Schema angewendet werden. Das folgende Beispiel zeigt eine Berechnung eines Hashwertes für einen 7-Bit ASCII-String s.

$k \mod m = (\ldots (s_{1} \cdot 128 + s_{2}) \mod m) \cdot 128 + s_{3}) \mod m) \cdot 128 + \ldots + s_{l-1}) \mod m) \cdot 128 + s_{l}) \mod m$

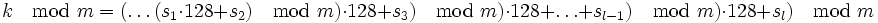
Somit kann als Zwischenergebnis maximal $\left(m - 1\right) \cdot 128 + 127$ auftreten.

In Pseudocode würde dies in etwa so aussehen:

h = s[1] mod m
for i in 2...l:
   h = (h * 128 + s[i]) mod m

Die Multiplikation mit 128 = 2^7 entspricht der Links-Bitshiftoperation << 7.

Einzelnachweise

1. ↑ Cormen et. al.: Introduction to Algorithms. 2. Auflage. MIT Press, 2001, ISBN 0-262-03293-7, S. 231. 

Literatur

• Donald E. Knuth: The Art of Computer Programming Volume 3. 2. Auflage. Addison Wesley, 1998, ISBN 0-201-89685-0, S. 515.