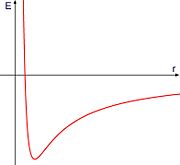
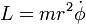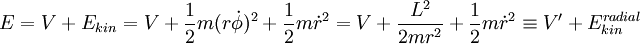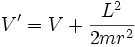Effektives Potenzial

Effektives Potential im Gravitationsfeld

Das effektive Potenzial ist ein Begriff aus der Mechanik, der bei der Behandlung von Zentralkräften, wie der Gravitationskraft bei der Planetenbewegung nützlich ist. Dabei wird die azimutale Bewegungsenergie mit der potentiellen Energie in das effektive Potential vereinigt.

Ein Körper, der sich in einem Zentralkraftfeld im Abstand r vom Kraftzentrum bewegt, hat aufgrund seines Drehimpulses

$L=mr^2\dot{\phi}$

ein effektives Potenzial V', das sich aus seiner potenziellen Energie V und dem Drehimpuls zusammensetzt:

$E=V+E_{kin}=V+\frac{1}{2}m(r\dot{\phi})^2+\frac{1}{2}m\dot{r}^2=V+\frac{L^2}{2 m r^2}+\frac{1}{2}m\dot{r}^2\equiv V' + E_{kin}^{radial}$

$V' = V + \frac{L^2}{2 m r^2}$

Den zweiten Term auf der rechten Seite dieser Gleichung bezeichnet man auch als Zentrifugalpotential.

Das Minimum des effektiven Potenzials bestimmt die Keplersche Bahnkurve des Körpers.

Siehe auch: Zentralfeld, Zentralbewegung