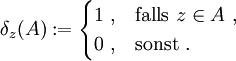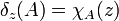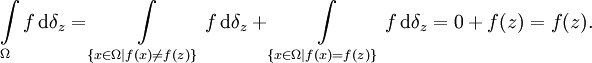Einpunkt-Maß

Das Diracmaß, benannt nach dem Physiker Paul Dirac, ist ein Mengenmaß der Maßtheorie. Jedem Punkt 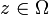$z\in\Omega$ wird sein Diracmaß (auch Punktmaß) δ_z zugeordnet, indem man festlegt, dass jede Menge 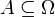$A\subseteq \Omega$ das Maß 1 hat, wenn sie den Punkt z enthält, und das Maß 0, wenn sie ihn nicht enthält:

$\delta_z(A) := \begin{cases} 1\ , & \text{falls } z \in A\ , \\ 0\ , & \mathrm{sonst}\ . \end{cases}$

Mit Hilfe der charakteristischen Funktion χ, kann man diesen Sachverhalt auch durch

$\,\delta_z(A) = \chi_A(z)$

ausdrücken.

Beim Diracmaß δ_z ist die Einheitsmasse im Punkt z konzentriert. Es lässt sich in jedem messbaren Raum 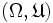$(\Omega,\mathfrak{U})$ definieren und macht diesen zum Maßraum 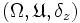$(\Omega,\mathfrak{U},\delta_z)$, sogar zu einem Wahrscheinlichkeitsraum, da die Gesamtmasse δ_z(Ω) = 1 ist. Daraus folgt trivialerweise, dass das Maß endlich ist, insbesondere ist der Maßraum σ-endlich.

Integral

Falls z in Ω liegt, gilt

$\begin{align} \int\limits_\Omega f\,\mathrm d\delta_z = \int\limits_{\{x\in \Omega \mid f(x) \ne f(z)\}}f\,\mathrm d\delta_z + \int\limits_{\{x\in \Omega \mid f(x) = f(z)\}} f\,\mathrm d\delta_z = 0 + f(z) = f(z). \end{align}$

Siehe auch

• Zählmaß
• Lebesgue-Maß
• Delta-Distribution

Literatur

• Elliott H. Lieb & Michael Loss: Analysis, American Mathematical Society, Second Edition, 2001, ISBN 0-8218-2783-9