Eisenstein-Polynom

Das Eisensteinkriterium oder auch Irreduzibilitätskriterium von Eisenstein ist in der Algebra ein Kriterium um nachzuweisen, ob ein gegebenes Polynom ein irreduzibles Polynom ist. Es lassen sich damit leichter Aussagen über die Teilbarkeit von Polynomen treffen. Es ist benannt nach dem Mathematiker Gotthold Eisenstein, der dazu 1850 einen öffentlichkeitswirksamen Aufsatz in Crelles Journal (Ausgabe 39) verfasste. Schon vier Jahre zuvor wurde es zum ersten Mal ebenda von T. Schönemann veröffentlicht (Ausgabe 32).

Das Kriterium

Sei P(x) ein Polynom mit ganzzahligen Koeffizienten, also $P(x)=a_n x^n + \cdots + a_1 x+ a_0 \in \mathbb Z[x]$.

Wenn eine Primzahl p existiert, die alle Koeffizienten a₀ bis a_{n − 1} teilt, den Koeffizienten a₀ jedoch nicht quadratisch und a_n gar nicht teilt, also

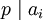$p \mid a_i$ für alle i < n,

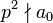$p^2 \nmid a_0$ und

$p \nmid a_n$,

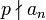dann ist P(x) in $\mathbb Q[x]$ irreduzibel.

Verallgemeinerung

Sind die Koeffizienten aus einem faktoriellen Ring F und existiert ein entsprechendes Primelement 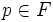$p \in F$, so ist das Polynom irreduzibel im Polynomring des Quotientenkörpers von F.

Bemerkungen

• Ein Polynom, für das ein solches p existiert, wird auch Eisenstein-Polynom bezüglich p genannt.
• Das Kriterium ist nur hinreichend; auch wenn es nicht erfüllt ist, kann das Polynom irreduzibel sein. Auch die Zerlegbarkeit eines Polynoms kann damit nicht nachgewiesen werden.
• Insbesondere für eine Zerlegung in $\mathbb Z[x]$ kann man das Kriterium nur indirekt benutzen. Es gilt natürlich: P(x) normiert und irreduzibel in $\mathbb Q[x] \Rightarrow P(x)$ irreduzibel in $\mathbb Z[x]$. Fasst man das Polynom also als diophantische Gleichung in einer Variablen auf, so lässt sich folgern: Ist das Kriterium für P(x) erfüllt, so gibt es auch keine ganzzahlige Lösung der Gleichung.
• Allerding lässt sich (unabhängig vom Kriterium) leicht zeigen, dass auch die Umkehrung gilt: P(x) irreduzibel in $\mathbb Z[x] \Rightarrow P(x)$ irreduzibel in $\mathbb Q[x]$.^[1]

Beispiele

• x³ + 6x² + 4x + 2 ist mit obigem Kriterium irreduzibel über $\mathbb Q$. D.h., dass die Nullstelle, die das Polynom (als reelle Funktion aufgefasst) hat, irrational sein muss.
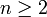• xⁿ − d ist irreduzibel in $\mathbb Q[x]$, wenn d eine Primzahl ist bzw. nur einfache und keine mehrfachen Primteiler hat. Insbesondere kann $\sqrt[n]{2}$ für kein $n \geq 2$ rational sein.
• x² + 4 erfüllt das Kriterium nicht und ist irreduzibel, x² − 4 erfüllt das Kriterium genauso wenig, ist aber zerlegbar in (x + 2)(x − 2).

Beweis

Der Beweis läuft per Widerspruch: Angenommen, P wäre ein Eisensteinpolynom bezüglich p und es gäbe zwei nicht-konstante Polynome Q und R mit 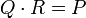$Q \cdot R = P$. Da nach Voraussetzung alle a_i bis auf den Leitkoeffizienten a_n durch p teilbar sind, gilt folgendes Modulo-Argument: 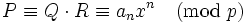$P \equiv Q \cdot R \equiv a_nx^n \pmod{p}$. Damit müssen auch Q und R Monome modulo p sein, d. h., auch alle ihre sonstigen Koeffizienten sind durch p teilbar. Insbesondere die konstanten Terme von Q und R sind jeweils durch p teilbar. Da aber 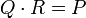$Q \cdot R =P$ gilt, folgt mit dem Cauchy-Produkt, dass der konstante Term a₀ von P durch p² teilbar sein muss – Widerspruch dazu, dass das Kriterium für P erfüllt war. Damit muss P irreduzibel sein, und das war gerade zu zeigen.

Betrachtet man allgemein Polynome über einem faktoriellen Ring F, so muss das Modulo-Argument durch einen geeigneten Homomorphismus ersetzt werden, der P auf seine entsprechende Restklasse in F / pF abbildet. Da F faktoriell ist und p ein Primelement, lässt sich der Homomorphismus leicht finden. Die Linearität erlaubt dann analog die Folgerung, dass P und Q jeweils selbst auf ein Monom abgebildet werden.^[2],^[3]

Siehe auch

• Polynomdivision

Einzelnachweise

1. ↑ Jürgen Wolfart: Einführung in die Algebra und Zahlentheorie. Vieweg Verlag, 1996, Seite 143, ISBN 978-3528072865.
2. ↑ Irreduzibles_Polynom&oldid=41533299#Beweis (23.5.08)
3. ↑ Jürgen Wolfart: Einführung in die Algebra und Zahlentheorie. Vieweg Verlag, 1996, Seite 143, ISBN 978-3528072865.

Literatur

• Jürgen Wolfart: Einführung in die Algebra und Zahlentheorie. Vieweg Verlag, 1996, Seite 143, ISBN 978-3528072865.