Fundamentalsatz der Arithmetik

Die Primfaktorzerlegung ist die Darstellung einer natürlichen Zahl n als Produkt von Primzahlen. Diese Darstellung ist bis auf die Reihenfolge der Faktoren eindeutig. Sie zählt zu den grundlegenden und klassischen Werkzeugen der Zahlentheorie.

Definitionen

Sei n eine natürliche Zahl. Eine Zahl p heißt Primfaktor von n,

wenn p ein Teiler von n ist und

p eine Primzahl ist.

Die Primfaktorzerlegung ist das Produkt der N Primfaktoren von n:

$n= p_1 \cdot \ldots \cdot p_N = \prod_{k=1}^{N}p_k$ .

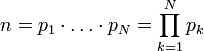Die Primfaktorzerlegung hängt dabei nicht von der Reihenfolge der Faktoren ab, da die Multiplikation kommutativ ist. Da Eins keine Primzahl ist, hat sie auch keinen Primfaktor. Ihre Primfaktorzerlegung kann als leeres Produkt betrachtet werden. Wenn n selbst eine Primzahl ist, so ist es gleichzeitig selbst sein einziger Primfaktor. Gibt es mehr als einen Primfaktor, so wird n zusammengesetzte Zahl genannt. Die Null ist niemals Teil der multiplikativen Gruppe und wird von solchen Betrachtungen ausgeschlossen.

Mehrfach auftretende Primfaktoren können mittels Exponenten-Schreibweise zusammengefasst werden. Sind die Primfaktoren aufsteigend geordnet, spricht man auch von der kanonischen Primfaktorzerlegung:

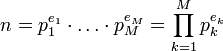$n=p_1^{e_1} \cdot \ldots \cdot p_M^{e_M} = \prod_{k=1}^{M} p_k^{e_k}$, wenn unter den N Primfaktoren M verschiedene sind.

Den Exponenten e_k eines Primfaktors p_k nennt man auch „Vielfachheit von p_k in n“ oder „p_k-Bewertung von n“ (siehe Bewertungstheorie). Er gibt an, wie oft n durch p_k teilbar ist.

Beispiele für Primfaktorzerlegungen

$30 = 2 \cdot 3 \cdot 5$

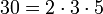
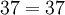$37 = 37 \$ (Primzahl)

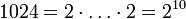$1024 = 2 \cdot \ldots \cdot 2 = 2^{10}$ (Zweierpotenz)

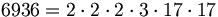$6936 = 2 \cdot 2 \cdot 2 \cdot 3 \cdot 17 \cdot 17$, mit der kanonischen Darstellung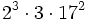 $2^3 \cdot 3 \cdot 17^2$

Fundamentalsatz der Arithmetik

Die Aussagen für Existenz der Primfaktorzerlegung für jede natürliche Zahl und deren Eindeutigkeit in der kanonischen Darstellung sind der Fundamentalsatz der Arithmetik. Beide Aussagen werden getrennt formuliert und bewiesen. Die Beweise sind zahlentheoretisch elementar, werden klassisch als Widerspruchsbeweis formuliert und nutzen die Wohlordnung der natürlichen Zahlen. Zum ersten Mal vollständig und korrekt bewiesen findet sich der Fundamentalsatz der Arithmetik in den Disquisitiones Arithmeticae von Carl Friedrich Gauß. Er war aber bereits - wenn auch in leicht abgewandelter Form - Euklid bekannt.

Existenz

Um die Existenz einer Primfaktorzerlegung zu zeigen werden die positiven natürlichen Zahlen zweckmäßigerweise in drei Gruppen unterteilt: die Eins, die Primzahlen und der Rest, die zusammengesetzten Zahlen. Die Eins entspricht definitionsgemäß dem leeren Produkt. Jede Primzahl ist gleich dem Produkt aus nur einem Faktor: der Primzahl selbst. Es bleibt noch zu zeigen, dass sich auch die zusammengesetzten Zahlen als Produkt von Primzahlen darstellen lassen.

Angenommen es gäbe zusammengesetzte Zahlen, die sich nicht als Produkt von Primzahlen darstellen ließen, dann gäbe es auch eine kleinste solche Zahl. Diese Zahl sei n. Da n weder die Eins noch eine Primzahl ist, besitzt sie einen Teiler a mit 1 < a < n und lässt sich deshalb als Produkt 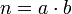$n = a \cdot b$ mit 1 < b < n schreiben. Da es sich dabei nicht um das Produkt zweier Primzahlen handelt, muss a oder b eine zusammengesetzte Zahl sein. Diese Zahl wäre kleiner als n und stände damit im Widerspruch zu Annahme, dass n die kleinste zusammengesetzte Zahl ist.

Eindeutigkeit

Gäbe es unterschiedliche Zerlegungen von natürlichen Zahlen, könnte die kleinste Zahl mit unterschiedlichen Zerlegungen betrachtet werden. Dies führt zu einem Widerspruch, da gezeigt werden kann, dass in diesem Fall diese kleinste Zahl dividiert durch einen Primfaktor ebenfalls mehrere Zerlegungen haben muss. Dies folgt aus einem Hilfssatz: Teilt eine Primzahl ein Produkt, so auch einen der Faktoren.^[1] Dieser ist wiederum eine Folgerung aus dem Lemma von Bézout und dient als Grundlage für eine verallgemeinerte Definition von Primzahlen, den Primelementen.

Eigenschaften

• Bisher lässt die Primfaktorzerlegung von n keinerlei Rückschluss zu auf Zerlegung von n + 1, verwandt mit dieser Fragestellung sind Primzahlzwillinge bzw. Primzahllücken.
• Um die Primfaktorzerlegung einer Zahl zu berechnen, stehen mehrere Faktorisierungsverfahren zur Verfügung, die nichttriviale Teiler ganzer Zahlen berechnen. Diese Aufgabenstellung ist als Faktorisierungsproblem für ganze Zahlen bekannt und kann mit den bisher bekannten Methoden nicht effizient berechnet werden, worauf weltweit Sicherheitskonzepte beruhen, insbesondere in der modernen Kryptographie. Siehe auch Primzahltest.
• Hardy bewies mehrere erstaunliche statistische Erkenntnisse zum Thema, unter anderem dass die durchschnittliche Anzahl von Primfaktoren für größer werdendes n nur sehr langsam anwächst und zwar wie lnlnn, also der doppelt angewendete natürliche Logarithmus. Der Satz von Erdős-Kac besagt darüber hinaus, dass die Anzahl der Primfaktoren asymptotisch normalverteilt ist mit einem Erwartungswert 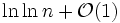$\ln \ln n + \mathcal{O}(1)$ und einer Standardabweichung 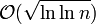$\mathcal{O}( \sqrt{\ln \ln n})$.^[2] (Zur Notation siehe Landau-Symbole.)

Verallgemeinerung

Es gibt mehrere Möglichkeiten, Primzahlen zu verallgemeinern. Die bekannteste Anwendung sind die ganzen Zahlen, Primzahlen können dort auch ein negatives Vorzeichen haben. Andererseits ist dies schon ein spezielles Beispiel, da auch dort die Primfaktorzerlegung im Wesentlichen eindeutig ist.

Ein allgemeiner Ansatz verlangt mindestens einen Begriff der Teilbarkeit innerhalb der mathematischen Struktur. David Hilbert bewies, dass für die gewünschte Eindeutigkeit eine additive Struktur zwingend notwendig ist. Üblicherweise wird von einem kommutativen Ring mit Eins ausgegangen, dort können Primelemente definiert werden, ist der Ring auch noch nullteilerfrei (also ein Integritätsbereich), so gibt es zusätzlich irreduzible Elemente, die nicht prim genannt werden können. Sie werden anders definiert, sind aber trotzdem unzerlegbar und enthalten die Primelemente als echte Teilmenge.

Eine im wesentlichen eindeutige Zerlegung bedeutet ohne Beachtung der Reihenfolge der Faktoren (da der Ring kommutativ ist) und Multiplikation mit Einheiten (bei ganzen Zahlen ist das − 1, wodurch das Vorzeichen bestimmt wird.) In allgemeinen Integritätsbereichen kann man nicht von Primfaktorzerlegungen sprechen, da diese Eindeutigkeit nicht gegeben ist. Stattdessen spricht man von Zerlegungen in irreduzible Faktoren. Man muss deren Eindeutigkeit explizit fordern, was zur Definition von faktoriellen Ringen führt. Mit dieser Forderung lässt sich dann aber dort auch schon die Äquivalenz von irreduzibel und prim folgern: Faktorielle Ringe sind ZPE-Ringe. Ein etwas anderer Ansatz wird mit Primidealen verfolgt.

Beispiele

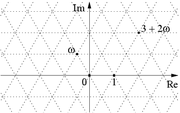Auch auf dem Dreiecksgitter der Eisenstein-Zahlen existiert für jeden Gitterpunkt eine Primfaktorzerlegung

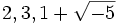• In dem Integritätsbereich $\mathbb Z[\sqrt{-5}]$ sind die Elemente $2,3,1+\sqrt{-5}$ irreduzibel und keine zwei sind zueinander assoziiert. Aber es gilt: 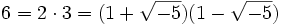$6=2\cdot 3=(1+\sqrt{-5})(1-\sqrt{-5})$. Man kann also nicht von einer Primfaktorzerlegung sprechen.
• Ein irreduzibles Polynom heißt Primpolynom, wenn der Leitkoeffizient gleich 1 ist. Im Polynomring K[x] über einem Körper K ist jedes nichtkonstante Polynom im wesentlichen eindeutig als Produkt von Primpolynomen darstellbar.^[3]
• Sowohl in den gaußschen Zahlen als auch den Eisenstein-Zahlen existiert stets eine Primfaktorzerlegung, natürlich außer für die 0. Wegen der fehlenden Ordnungsstruktur auf den komplexen Zahlen kann man jedoch nicht so einfach eine Darstellung als kanonisch bezeichnen, durch die jeweils vier Einheiten, die in beiden Ringen existieren, wird es noch unübersichtlicher.

Einzelnachweise

1. ↑ Jürgen Wolfart: Einführung in die Algebra und Zahlentheorie. 1 Auflage. Vieweg Verlag, 1996, ISBN 3528072866, S. 6-7. 
2. ↑ Thomas Kantke: Billige und teure Zahlen. In: Spektrum der Wissenschaft - SPEZIAL: Omega. Nr. 4/2003, Spektrum, Heidelberg 2003, S. 68-74. 
3. ↑ Jürgen Wolfart: Einführung in die Algebra und Zahlentheorie. 1 Auflage. Vieweg Verlag, 1996, ISBN 3528072866, S. 72, 37. 

Literatur

• Jürgen Wolfart: Einführung in die Algebra und Zahlentheorie. 1 Auflage. Vieweg Verlag, 1996, ISBN 3528072866. 

Weblinks

• Factorization database von Markus Tervooren - schnelle Verarbeitung, bis zu 200.000 Dezimalstellen
• Die Primzahlseite von Arndt Brünner - benötigt JavaScript, enthält u.a. Primfaktorzerlegung
• Prime factorisation by Henry Bottomley (1998) - benötigt JavaScript, verarbeitet Eingaben bis ca. 17 Dezimalstellen
• Factorization using the Elliptic Curve Method - Java-Applet, verarbeitet Eingaben bis 10.000 Dezimalstellen