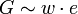- Emmert'sches Gesetz
-
Das Emmertsche Gesetz beschreibt einen quantitativen Zusammenhang zwischen der Bildgröße eines Objektes auf der Netzhaut, seiner Entfernung und der wahrgenommenen Größe.
Emil Emmert (1844–1911) entdeckte es 1881. Er experimentierte mit Nachbildern und erkannte, dass sich ihre wahrgenommene Größe trotz unveränderter Größe auf der Netzhaut proportional zur Entfernung des jeweils betrachteten Hintergrundes veränderte. Diese Erkenntnis lässt sich auf die Größenwahrnehmung allgemein anwenden. Der Zusammenhang lautet:
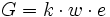
- Worin G die wahrgenommene Größe, k ein Proportionalitätsfaktor, w der Winkel, unter dem das betrachtete Objekt erscheint und e die Objektentfernung sind.
Der Proportionalitätsfaktor k ist ein unbestimmter Wert, der für diese Betrachtung auch fortgelassen werden kann; die menschliche Größenwahrnehmung ist ja nicht absolut sondern relativ. Bei Schätzungen wird die Größe aus dem Vergleich mit Objekten bekannter Größe abgeleitet; fehlen diese, kann keine fundierte Schätzung abgegeben werden. In Worten: die wahrgenommene Größe eines Objektes ist proportional zum Produkt von Entfernung e und Winkelgröße w, auch scheinbare Größe genannt. Hierbei kann der Winkel w des Objektes durch die Größe seines Netzhautbildes ersetzt werden:
Bei Veränderung der Entfernung wird auch w verändert; bei Verdoppelung von e sinkt w auf die Hälfte. Ihr Produkt bleibt dabei konstant. Dies bewirkt die Wahrnehmung einer (in Grenzen) entfernungsunabhängig konstanten Objektgröße, der Effekt wird als Größenkonstanz bezeichnet. Dabei erscheint das Objekt in zutreffenden Relationen zu den anderen Objekten, in einer relativen Größe - eine wichtige Voraussetzung einer fundierten Größenschätzung.
Ohne näher auf die Methoden der Augen zur Entfernungsermittlung einzugehen kann man feststellen, dass die Wahrnehmung von Größenkonstanz und zutreffenden Größenverhältnissen eine weitgehend zutreffende Entfernungsermittlung beziehungsweise von Äquidistanz erfordert. Absolute Entfernungen werden überhaupt nicht ermittelt. Bei äquidistanten Objekten reduziert sich die Emmertsche Formel auf
- G˜w
weil zutreffende relative Größen gleichweit entfernter Objekte sich direkt aus dem Vergleich ihrer scheinbaren Größen ableiten lassen. Die Feststellung der Äquidistanz - ohne Kenntnis der Entfernungen - ist eine Leistung der Tiefensehschärfe; sie reicht bei menschlichen Augen maximal bis in den einstelligen Kilometerbereich.
Die Anwendung des Emmertschen Gesetzes ist nicht in den Wahrnehmungsregeln verankert. Die Ausrichtung der visuellen Wahrnehmung auf die Realität ist kein Zufall sondern notwendig und das Emmertsche Gesetz beschreibt diese Realität mathematisch. Beides stimmt auffällig gut überein, was zwar auf eine gewisse Realitätsnähe, nicht aber auf die innere Methodik Rückschlüsse erlaubt, auf welche Weise Wahrnehmung konstruiert wird. Dies erfordert die Erfüllung einer ganzen Reihe zum Teil nicht vollständig bekannter Voraussetzungen. Eine dieser Voraussetzungen ist etwa das Vorhandensein einer Mindestzahl anderer Objekte, was die Relativität der visuellen Wahrnehmung unterstreicht.[1]
Ein klarer Verstoß gegen das Emmertsche Gesetz ist festzustellen bei manchen Widersprüchen zwischen der ermittelten Entfernung und gewissen Bildinhalten. Diese geben qualitative Hinweise auf verschiedene Entfernungen, zum Beispiel aktive/passive Bedeckung, Farbveränderungen durch atmosphärischen Dunst, Perspektive, Fußpunktlagen und eine mit der Entfernung feiner werdende Textur der Landschaft, wobei sich unter Umständen die wahrnehmbare relative Größe von derjenigen nach Emmert unterscheidet oder ihre Konstruktion ganz unterbleibt. Die Folge ist eine auf die scheinbare Größe reduzierte Wahrnehmung der Objekte, wodurch je nach Situation erhebliche Größentäuschungen ausgelöst - oder auch vermieden werden können.[2]
Siehe auch
Literatur
- Emil Emmert: Grössenverhältnisse der Nachbilder. In: Klinische Monatsblätter für Augenheilkunde. 19, 1881, S. 443–450.
- J. Dwyer, R. Ashton u. a.: Emmert's Law in the Ames Room. In: Perception. 19, 1990, S. 35–41
Einzelnachweise
Wikimedia Foundation.