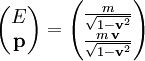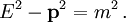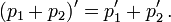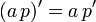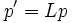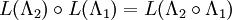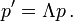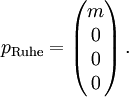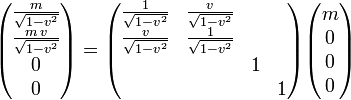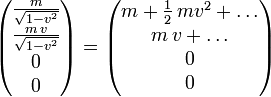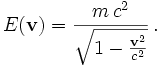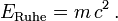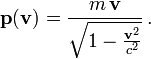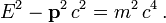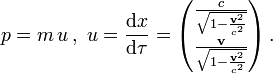Energie-Impuls-Beziehung

Als Viererimpuls eines Teilchens bezeichnet man in der relativistischen Physik zusammenfassend seine Erhaltungsgrößen Energie und Impuls. In Maßeinheiten, in denen die Lichtgeschwindigkeit den dimensionslosen Wert c = 1 hat, hängen die Energie E und der Impuls 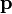$\mathbf p$ eines Teilchens der Masse m mit seiner Geschwindigkeit 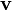$\mathbf v$ einfach durch

$\begin{pmatrix} E\\ \mathbf p \end{pmatrix} = \begin{pmatrix} \frac{m}{\sqrt{1-\mathbf v^2}}\\\frac{m\,\mathbf v}{\sqrt{1-\mathbf v^2}} \end{pmatrix}$

zusammen. Das Längenquadrat des Viererimpulses ist unabhängig von der Geschwindigkeit gleich dem Quadrat der Masse,

$E^2 - \mathbf p^2 = m^2\,.$

Herleitung der Geschwindigkeitsabhängigkeit von Energie und Impuls

Wie die Energie und der Impuls eines Teilchens der Masse m von seiner Geschwindigkeit 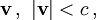$\mathbf v\,,\ |\mathbf v|<c\,,$ abhängen, ergibt sich in der Relativitätstheorie daraus, dass Energie und Impuls für jeden Beobachter additive Erhaltungsgrößen sind.

Wir bezeichnen sie zusammenfassend mit p. Wenn einem Teilchen eine additive Erhaltungsgröße p₁ zukommt und einem anderen Teilchen die Erhaltungsgröße p₂, dann kommt dem System beider Teilchen die Erhaltungsgröße p = p₁ + p₂ zu.

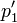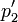Auch ein bewegter Beobachter stellt bei beiden Teilchen Erhaltungsgrößen $p^\prime_1$ und $p^\prime_2$ fest, allerdings haben sie nicht unbedingt dieselben, sondern transformierte Werte. Es muss aber gelten, dass die Summe dieser Werte das Transformierte der Summe ist,

$(p_1+p_2)^\prime=p_1^\prime + p_2^\prime\,.$

Ebenso kommt (für alle Zahlen a) einem vervielfachten System mit Erhaltungsgröße 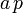$a\,p$ für den bewegten Beobachter die vervielfachte Erhaltungsgröße

$(a\,p)^\prime=a\,p^\prime$

zu. Das besagt mathematisch, dass die Erhaltungsgrößen, die ein bewegter Beobachter misst, durch eine lineare Transformation

$p^\prime = L p$

mit den Erhaltungsgrößen des ruhenden Beobachters zusammenhängen.

Die lineare Transformation L ist dadurch eingeschränkt, dass solch eine Gleichung für jedes Paar von Beobachtern gelten muss, wobei die Bezugssysteme der Beobachter durch Lorentztransformationen Λ und Verschiebungen auseinander hervorgehen. Hängen die Bezugssysteme vom ersten und zweiten Beobachter durch Λ₁ und vom zweiten zu einem dritten durch Λ₂ zusammen, dann hängt das Bezugssystem vom ersten mit dem dritten durch $\Lambda_2\circ\Lambda_1$ zusammen. Genauso müssen die zugehörigen Transformationen der Erhaltungsgrößen

$L(\Lambda_2)\circ L(\Lambda_1)= L(\Lambda_2\circ \Lambda_1)$

erfüllen.

Im einfachsten Fall ist L(Λ) = Λ. Da Lorentztransformationen 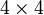$4\times 4$-Matrizen sind, betrifft also das einfachste, nichttriviale Transformationsgesetz, bei dem nicht einfach 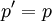$p^\prime=p$ gilt, vier Erhaltungsgrößen p, die wie die Raumzeitkoordinaten, als Vierervektor, transformieren,

$p^\prime = \Lambda p\,.$

Im Vorgriff auf das Ergebnis unserer Betrachtung nennen wir diesen Vierervektor den Viererimpuls.

Insbesondere ändert sich ein ruhendes Teilchen nicht bei Drehungen. Daher ändern sich auch nicht diejenigen Komponenten seines Viererimpulses p, die wie ein dreidimensionaler Ortsvektor bei Drehungen in einen gedrehten Vektor übergehen. Der einzige solche Vektor ist aber der Nullvektor. Also hat der Viererimpuls p eines ruhenden Teilchen einen Wert

$p_{\text{Ruhe}}=\begin{pmatrix} m \\ 0 \\ 0 \\ 0 \end{pmatrix}\,.$

Die Bezeichnung m ist im Vorgriff auf das spätere Ergebnis gewählt, steht hier aber zunächst für irgend einen Wert.

Für einen entlang der x-Achse bewegten Beobachter hat das Teilchen eine Geschwindigkeit v und einen Lorentztransformierten Viererimpuls (wir rechnen einfachheitshalber in Maßsystemen mit c = 1)

$\begin{pmatrix} \frac{m}{\sqrt{1-v^2}} \\\frac{m\,v}{\sqrt{1-v^2}} \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} \frac{1}{\sqrt{1-v^2}} & \frac{v}{\sqrt{1-v^2}} & &\\ \frac{v}{\sqrt{1-v^2}} & \frac{1}{\sqrt{1-v^2}} & &\\ & & 1 &\\ & & & 1 \\ \end{pmatrix} \begin{pmatrix} m \\ 0 \\ 0 \\ 0 \end{pmatrix}$

Entwickelt man die vier Erhaltungsgrößen nach der Geschwindigkeit

$\begin{pmatrix} \frac{m}{\sqrt{1-v^2}} \\\frac{m\,v}{\sqrt{1-v^2}} \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} m + \frac{1}{2}\,m v^2 + \dots\\ m\,v + \dots \\ 0 \\ 0 \end{pmatrix}$

und vergleicht man mit Newtons Mechanik, so enthüllt sich die physikalische Bedeutung der Komponenten des Viererimpulses: Die erste Komponente ist die Energie, die drei Komponenten, die sich bei Drehungen wie ein Ortsvektor ändern, sind der Impuls,

$p=\begin{pmatrix} \text{Energie}\\ \text{Impuls} \end{pmatrix}\,.$

So wie in Newtons Mechanik nennt man den geschwindigkeitsunabhängigen Parameter m in der Relation, die den Impuls eines Teilchens als Funktion seiner Geschwindigkeit angibt, die Masse. Sie muss allen Beobachtungen nach positiv sein.

Die Energie ist, wenn wir die konventionellen Faktoren c einfügen,

$E(\mathbf{v})= \frac{m\,c^2}{\sqrt{1-\frac{\mathbf v^2}{c^2}}}\,.$

Sie ist nach unten beschränkt und in Ruhe minimal

$E_{\text{Ruhe}}= m\,c^2\,.$

Der Impuls ist

$\mathbf{p}(\mathbf{v})= \frac{m\,\mathbf v}{\sqrt{1-\frac{\mathbf v^2}{c^2}}}\,.$

Nicht explizit geschwindigkeitsabhängig hängen Energie und Impuls durch die Energie-Impuls-Beziehung mit der Masse zusammen

$E^2 - \mathbf p^2\,c^2= m^2\,c^4\,.$

Spaltet man die Masse vom Viererimpuls ab, so verbleibt die Vierergeschwindigkeit 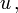$u\,,$ das ist die Ableitung der Weltlinie, die das Teilchen durchläuft, nach seiner Eigenzeit,

$p = m\,u \,,\ u=\frac{\mathrm d x}{\mathrm d \tau}=\begin{pmatrix} \frac{c}{\sqrt{1-\frac{\mathbf v^2}{c^2}}}\\ \frac{\mathbf v}{\sqrt{1-\frac{\mathbf v^2}{c^2}}} \end{pmatrix}\,.$

Die Vierergeschwindigkeit ist der normierte Tangentialvektor an die Weltlinie, $(u^0)^2-(\mathbf u)^2 = c^2\,.$

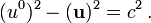
Andere Erhaltungsgrößen, der Drehimpuls und der anfängliche Energieschwerpunkt, transformieren unter einer sechsdimensionalen Darstellung L(Λ) der Lorentztransformationen.