Impuls

Physikalische Größe
Name	Impuls
Größenart	Impuls
Formelzeichen der Größe	p
Größen- und Einheiten- system Einheit Dimension SI N·s kg·m·s−1 M·L·T–1

Die physikalische Größe Impuls, auch als Bewegungsgröße oder Bewegungsmenge bezeichnet, beschreibt die Bewegung eines massebehafteten Körpers. Anschaulich entspricht der Impuls ungefähr der „Wucht“, die beim Verkehrsunfall zwischen einem LKW und einem PKW zu Tage tritt.

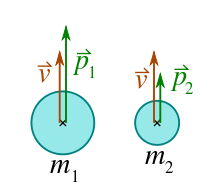
Der Impuls ist wie die mit ihm verknüpfte Geschwindigkeit eine Vektorgröße, hat also einen Betrag und weist in die Richtung der Bewegung. Seine besondere Bedeutung liegt darin, dass er eine Erhaltungsgröße ist (siehe Abschnitt Impulserhaltung). Jeder bewegliche Körper kann seinen Impuls, etwa bei einem Stoßvorgang, ganz oder teilweise auf andere Körper übertragen oder von anderen Körpern übernehmen. Auch Felder können durch Kraftwirkung Impuls von einem Teilchen zum anderen Teilchen übertragen.

Bemerkung zur Bezeichnung und zur Einheit

Im Internationalen Einheitensystem gibt es keine eigene Einheit für den Impuls, verwendet wird N·s = kg·m·s⁻¹.

Im Englischen wird der Impuls momentum genannt. Das englische impulse bezeichnet dagegen die Änderung des Impulses innerhalb einer bestimmten Zeit, also den Kraftstoß (siehe Abschnitt Kraftstoß).

Definition, Zusammenhänge mit Masse und Energie

Klassische Mechanik

Geschwindigkeit und Impuls

In der newtonschen Mechanik sind der Impuls $\vec{p}$ und die Geschwindigkeit $\vec{v}\,$ über die Masse m des Körpers verknüpft:

$\vec p = m \, \vec v\,$

Da die Masse ein Skalar darstellt, sind Impuls und Geschwindigkeit Vektoren mit gleicher Richtung.

Zudem lässt sich Impuls, Masse und kinetischer Energie folgender Zusammenhang bilden:

$E_{\text{kinetisch}} = \frac{\vec p^{\,2}}{2\, m}\,$.

Um die Geschwindigkeit eines Körpers zu ändern, muss Impuls übertragen werden. Der pro Zeit übertragene Impuls $\vec{p}$ ist die Kraft $\vec{F}$:

$\frac{\mathrm d \vec{p}}{\mathrm d t} = \vec{F}\,$

Spezielle Relativitätstheorie

In der relativistischen Physik hängt der Impuls eines Körpers mit seiner Geschwindigkeit nicht linear zusammen (c ist die Lichtgeschwindigkeit):

$\vec p = \frac{m \, \vec v}{\sqrt{1-{v^2 \over c^2}}}\,,\ {v}^2< c^2\,$.

Mit der Masse und der Energie

$E = \frac{m c^2}{\sqrt{1-{v^2 \over c^2}}}$

besteht die Energie-Impuls-Beziehung

$E^2 - \vec p^{\,2}\, c^2=m^2\,c^4\,$.

Während in der klassischen Physik jeder Körper eine von Null verschiedene Masse hat, gilt die relativistische Energie-Impuls-Beziehung auch für masselose Teilchen wie Photonen. Sie bewegen sich stets mit Lichtgeschwindigkeit. Beim Photon hängt der Betrag des Impulses von seiner Wellenlänge λ ab:

$\,|\vec{p}_{\text{Photon}}| = \frac{h}{\lambda}$,

wobei h das plancksche Wirkungsquantum ist. Die Energie eines Photons ist bis auf einen Faktor c gleich dem Betrag seines Impulses:

$E_{\text{Photon}}= c\,|\vec{p}_{\text{Photon}}|\,$.

Die Energie und der Impuls, den gegeneinander bewegte Beobachter bei einem Körper feststellen, gehen durch eine Lorentztransformation auseinander hervor.

Die in Anlehnung an die Energiedichte w_F benannte Impulsdichte $\vec{\pi}_F$ des elektromagnetischen Feldes ist das Kreuzprodukt des elektrischen und des magnetischen Feldes

$\vec{\pi}_F = \frac{1}{c^2}\vec{E}\times\vec{H}\,$.

Mit c² multipliziert ist dies die Energiestromdichte, der Poynting-Vektor. Integriert man die Impulsdichte über ein Volumen, so erhält man den Impuls des elektromagnetischen Feldes in diesem Volumen.

Impulserhaltung

Anstoß beim Billard: Der Impuls der weißen Kugel verteilt sich auf alle Kugeln.

→ Hauptartikel: Impulserhaltungssatz

Der Impuls bildet eine Erhaltungsgröße, denn in einem abgeschlossenen System (genauer: abgeschlossenen Inertialsystem) bleibt der Gesamtimpuls, die Summe der aller im System auftretenden Einzelimpulse, konstant.

Der anfängliche Gesamtimpuls ist also auch gleich der Vektorsumme der zu irgendeinem späteren Zeitpunkt vorhandenen Einzelimpulse. Stöße und andere Vorgänge, bei denen sich die Geschwindigkeiten ändern, enden stets so, dass dieses Prinzip nicht verletzt wird. (siehe Kinematik).

Beim unelastische Stoß geht kinetische Energie durch plastische Verformung verloren. Der Impulserhaltungssatz ist vom Energieerhaltungssatz unabhängig und gilt sowohl bei elastischen als auch bei unelastischen Stößen.

Kraftstoß

Impulsänderung und Kraft-Zeit-Fläche

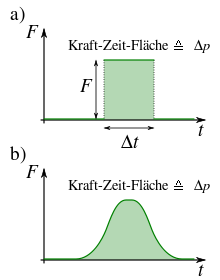
Aus der Kraft auf einen Körper und deren Einwirkungsdauer ergibt sich eine Impulsänderung und wird als Kraftstoß bezeichnet. Dabei spielen sowohl der Betrag als auch die Richtung der Kraft eine Rolle. Der Kraftstoß wird oft mit dem Formelzeichen $\vec I$ bezeichnet, seine SI-Einheit ist 1 N · s.

Ist die Kraft $\vec F$ im Zeitintervall Δt konstant, kann der Kraftstoß mittels folgender Gleichung berechnet werden:

$\vec I = \Delta \vec p = \vec F \cdot \Delta t$.

Ist $\vec F$ dagegen nicht konstant, kann man entweder mit einer mittleren Kraft rechnen oder aber, wenn $\vec F(t)$ bekannt ist, den Kraftstoß durch Integration ermitteln:

$\vec I = \Delta \vec p = \int \vec F(t) \cdot \mathrm{d}t$.

Impuls im Lagrange- und Hamilton-Formalismus

Im Lagrange- und Hamilton-Formalismus wird der generalisierte Impuls eingeführt; die drei Komponenten des Impulsvektors zählen zum generalisierten Impuls; aber auch beispielsweise der Drehimpuls.

Im Hamilton-Formalismus und in der Quantenmechanik ist der Impuls die zum Ort kanonisch konjugierte Variable. Der (generalisierte) Impuls wird in diesem Zusammenhang auch als kanonischer Impuls bezeichnet. Die möglichen Paare (q,p) von Ortskoordinaten q und kanonischen Impulsen p eines physikalischen Systems bilden in der hamiltonschen Mechanik den Phasenraum.

In Magnetfeldern enthält der kanonische Impuls eines geladenen Teilchens einen zusätzlichen Term, der mit dem Vektorpotential des B-Felds in Zusammenhang steht (siehe Generalisierter Impuls).

Impuls in strömenden Medien

Bei kontinuierlich verteilter Masse, wie beispielsweise in der Strömungsmechanik, enthält ein kleines Gebiet um den Punkt $\vec{x}$ die Masse $\rho(t,\vec{x})\,\mathrm d^3 x\,.$ Dabei ist d³x das Volumen des Gebietes. $\rho(t,\vec{x})$ ist die Massendichte am Ort $\vec{x}$. Sie kann sich mit der Zeit t ändern.

Der Impuls in diesem Gebiet ist Masse mal Geschwindigkeit $\rho(t,\vec{x})\,\vec{v}(t,\vec{x})\,\mathrm d^3 x$. Massendichte mal Geschwindigkeit ist also die Impulsdichte $\rho\, \vec{v}\,$.

Die Kontinuitätsgleichung

$\frac{ \partial (\rho\, \vec{v}) }{\partial t} + \sum_{i=1}^3 \frac{\partial}{\partial x^i} (\rho\, \vec{v}\,v^i) = \vec{f}$

besagt, dass sich der Impuls in einem kleinen Gebiet nur dadurch ändern kann, dass unausgeglichen Impulsstrom in das und aus dem Gebiet strömt und dass eine Kraft wirkt.

Hier ist der erste Term auf der linken Seite die Änderung der Impulsdichte mit der Zeit und der zweite Term beschreibt die räumliche Änderung des Impulsstromes. Die rechte Seite ist die auf das Volumenelement wirkende Kraftdichte; zum Beispiel der Gradient des Drucks oder das Gewicht, $\vec{f}_{\text{Gravitation}}=\rho\, \vec{g}\,$.

Siehe auch: Navier-Stokes-Gleichungen

Impuls in der Quantenmechanik

In der Quantenmechanik hat ein physikalischer Zustand normalerweise keinen genauen Impuls. Es kann nur die Wahrscheinlichkeit angegeben werden, dass der Impuls eines Teilchens in diesem oder jenem Bereich liegt. Entsprechendes gilt für den Ort. Für Impuls und Ort gilt die heisenbergsche Unschärferelation, nach der ein Teilchen nicht zugleich einen genauen Impuls und einen genauen Ort haben kann.

Eigenzustände des Impulsoperators sind ebene Wellen mit der Wellenlänge

$\lambda=\frac{h}{p}$,

wobei h das plancksche Wirkungsquantum ist. Die De-Broglie-Wellenlänge λ von Materiewellen freier Teilchen ist also durch den Impuls bestimmt. Hier ist zu beachten dass der Impuls in der Quantenmechanik dem kanonischen Impuls, also im allgemeinen nicht dem kinetischen Impuls, entspricht.

Siehe auch

• Kugelstoßpendel
• Kinematik

Literatur

• Feynman, Leighton, Sands: Lectures on Physics. Volume 1, 9 - 1, Reading, Ma., 1963.

Einzelnachweise