Erfüllbarkeitsproblem

Das Erfüllbarkeitsproblem der Aussagenlogik (SAT, von engl. satisfiability) ist ein Entscheidungsproblem. Es fragt, ob eine aussagenlogische Formel erfüllbar ist. Anwendungen finden sich unter anderem in der Komplexitätstheorie, Verifikation und im Entwurf von logischen Schaltungen. Insbesondere in der Komplexitätstheorie wird mit SAT auch nur der Spezialfall von Formeln bezeichnet, die in konjunktiver Normalform vorliegen.

Das Erfüllbarkeitsproblem der Aussagenlogik ist in exponentieller Zeit in der Anzahl der Variablen entscheidbar, zum Beispiel durch das Aufstellen einer Wahrheitstabelle. Ob es auch einen Algorithmus gibt, der SAT in polynomieller Zeit löst, ist nicht bekannt. Die Forschung beschäftigt sich mit der Entwicklung möglichst effizienter Verfahren (sogenannter SAT-Solver). Bekannte SAT-Solver sind Binäre Entscheidungsdiagramme, oder das Davis-Putnam-Verfahren. Manche Solver verwenden stochastische oder systematische Suchverfahren zur Entscheidung der Erfüllbarkeit. Das bekannteste und am meisten verbreitete Verfahren zur systematischen Suche ist (Stand 2008) das DPLL-Verfahren (Davis-Putnam-Logemann-Loveland), welches in den letzten Jahrzehnten mit Hilfe von Heuristiken und Lernverfahren stark verbessert wurde.

SAT gehört zur Klasse 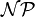$\mathcal{NP}$ der Probleme, die in polynomieller Zeit mit einer nichtdeterministischen Turingmaschine gelöst werden können. Die noch ungelöste Frage, ob SAT auch mit einer deterministischen Turingmaschine (also mit einem herkömmlichen Rechner) in polynomialer Zeit gelöst werden kann, kann man formulieren als: Gilt $\mbox{SAT} \in \mathcal{P}$?

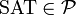Das Erfüllbarkeitsproblem der Aussagenlogik ist NP-vollständig. Das besagt, dass jedes Problem aus 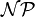$\mathcal{NP}$ in polynomieller Zeit auf SAT zurückgeführt werden kann (Polynomialzeitreduktion). Anfang der 1970er Jahre zeigten Stephen A. Cook und Leonid Levin unabhängig voneinander diese Eigenschaft, bekannt als der Satz von Cook. Cook zeigte hierfür einen Algorithmus auf, mit dem die Berechnungsschritte einer nicht-deterministischen Turingmaschine in Aussagenlogik formuliert und damit auf SAT reduziert werden können. Richard Karp zeigte 1972 die NP-Vollständigkeit weiterer Probleme. Er prägte damit das heutige Verständnis von NP-Vollständigkeit.

Falls also 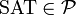$\mbox{SAT} \in \mathcal{P}$ gilt, dann ist jedes Problem aus 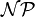$\mathcal{NP}$ auch in 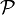$\mathcal{P}$, das heißt, dann gilt 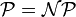$\mathcal{P} = \mathcal{NP}$. Auch die umgekehrte Richtung der Implikation gilt. Das P-NP-Problem "gilt 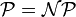$\mathcal{P} = \mathcal{NP}$ oder nicht?" ist eine der großen ungelösten Fragen der Komplexitätstheorie. Ist ein Problem NP-vollständig, so darf man annehmen, dass die Suche nach einem Polynomialzeit-Algorithmus dafür aussichtslos ist.

Varianten von SAT

SAT kann auf viele Weisen durch Einschränkungen und Verallgemeinerungen variiert werden. Das Problem 3-SAT ist eine Variante, die höchstens drei Literale pro Klausel enthält. Trotz der Einschränkung ist auch 3-SAT NP-vollständig, denn SAT lässt sich in polynomieller Zeit auf 3-SAT reduzieren.

Jedes 3-SAT mit p Variablen und q Klauseln lässt sich auf einen Graphen G mit p+q Knoten abbilden, in dem alle Variablenknoten mit denjenigen Klauselknoten verbunden sind, in denen sie vorkommen. Eine Formel ist in P3SAT, wenn sie in 3-SAT ist, und der Graph planar ist. Auch P3SAT ist NP-vollständig.

Zu vielen weiteren Komplexitätsklassen gibt es Varianten von SAT, die bezüglich dieser Klassen vollständig sind. Beispielsweise ist die Variante 2-SAT NL-vollständig. Das HORNSAT-Problem ist P-vollständig. Die Erweiterung der aussagenlogischen Formeln durch die Einführung von Quantoren führt zu QBF (auch QSAT genannt), einem PSPACE-vollständigen Problem.

Siehe auch

• Resolution (Logik)
• Circuit Value Problem

Quellen

• Christos H. Papadimitriou: Computational Complexity. Addison Wesley, ISBN 978-0201530827