PSPACE-Vollständigkeit

In der Komplexitätstheorie bezeichnet PSPACE die Klasse der Entscheidungsprobleme, die von deterministischen Turingmaschinen mit polynomiellem Platz entschieden werden können. Nach dem Satz von Savitch ist PSPACE gleich der Klasse NPSPACE, der Klasse der auf polynomiellen Platz von einer nichtdeterministischen Turingmaschine entscheidbaren Probleme.

Das Verhältnis zu anderen bekannten Komplexitätsklassen ist wie folgt:

NC $\subseteq$ P $\subseteq$ NP $\subseteq$ PSPACE

NC $\subset$ PSPACE

Es wird vermutet, dass alle der obigen Inklusionen echt sind:

NC $\subset$ P $\subset$ NP $\subset$ PSPACE

Die Inklusion NP 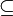$\subseteq$ PSPACE ergibt sich daraus, dass lediglich für ein beliebiges NP-schweres Problem gezeigt werden muss, dass es in PSPACE liegt: Dies ist zum Beispiel für SAT der Fall - es gibt zwar exponentiell viele Belegungen für die Variablen, aber jede einzelne dieser Belegungen kann in polynomiellem Platz abgespeichert werden. Somit können sämtliche Belegungen nacheinander aufgezählt und ausprobiert werden, wodurch SAT beantwortet werden kann, und somit auch sämtliche weiteren Probleme in NP.

Probleme in PSPACE

Es existieren viele Probleme in PSPACE, auf die sich alle anderen PSPACE-Probleme in Polynomialzeit reduzieren lassen. Von diesen so genannten PSPACE-vollständigen Problemen wird angenommen, dass sie nicht in NP liegen.

Das kanonische PSPACE-vollständige Problem ist das Erfüllbarkeitsproblem für quantifizierte boolesche Formeln.

Ein weiteres PSPACE-vollständiges Problem ist die Entscheidung, ob ein gegebenes Wort von einer gegebenen kontextsensitiven Grammatik erzeugt werden kann.

Komplexitätsklasse

Für die Komplexitätsklasse IP, die alle Entscheidungsprobleme enthält, die ein interaktives Beweissystem besitzen, gilt: IP = PSPACE

Weblinks

• PSPACE im Complexity Zoo (englisch)