Eulersche Linie

In kantendisjunkte Kreise zerlegter Eulergraph. Eine Eulertour der Knotenfolge (1,2,3,1,8,7,6,9,5,4,9,7,4,3,7,1) ist in alphabetischer Reihenfolge angegeben.

Ein Eulerkreis oder (geschlossener) Eulerzug (auch Eulertour oder Eulersche Linie) ist in der Graphentheorie ein Zyklus, der alle Kanten eines Graphen genau einmal enthält. Ein offener Eulerzug, (Eulerpfad oder auch Eulerweg) ist dann gegeben, wenn die Identität von Start- und Endknoten nicht verlangt wird, d.h. statt eines Zyklus wird lediglich ein Weg verlangt, der jede Kante des Graphen genau einmal enthält. Einen zusammenhängenden Graph, der einen Eulerkreis besitzt, bezeichnet man auch als eulersch.

Die Aufgabe, zu einem gegebenen Graph zu bestimmen, ob dieser eulersch ist oder nicht, bezeichnet man als Eulerkreis-Problem. Es geht auf das 1736 von Leonhard Euler gelöste Königsberger Brückenproblem zurück. Das Problem existiert auch für gerichtete Graphen und Graphen mit Mehrfachkanten.

Eigenschaften

Für ungerichtete Graphen sind folgende Aussagen äquivalent:

1. G ist eulersch,
2. G ist zusammenhängend und jeder Knoten hat geraden Grad.
3. G ist zusammenhängend und die Kantenmenge von G ist die Vereinigung aller Kanten von paarweise disjunkten Kreisen.

Analog sind für gerichtete Graphen folgende Aussagen äquivalent:

1. G ist eulersch,
2. G ist stark zusammenhängend und für jeden Knoten sind Eingangsgrad und Ausgangsgrad äquivalent.
3. G ist stark zusammenhängend und die Kantenmenge von G ist die Vereinigung aller Kanten von paarweise disjunkten gerichteten Kreisen.

Verallgemeinerung: Eulerweg

Ein (ungerichteter zusammenhängender) Graph enthält genau dann einen Eulerweg, wenn zwei oder keiner seiner Knoten von ungeradem Grad ist; hat kein Knoten ungeraden Grad, handelt es sich bei dem Eulerweg um einen Eulerkreis.

Entscheidungsproblem

Die Frage, ob für einen gegebenen Graph ein Eulerkreis existiert, lässt sich algorithmisch relativ leicht lösen, da ein Graph genau dann eulersch ist, wenn er zusammenhängend ist und jeder Knoten geraden Grad besitzt. Mittels Tiefensuche lässt sich dies leicht in linearer Zeit feststellen.

Auffinden eines Eulerkreises

Zum Auffinden eines Eulerkreises existieren mehrere Verfahren. Der Algorithmus von Fleury stammt aus dem Jahr 1883 und verfolgt einen sehr einfachen Ansatz, weshalb er eine Laufzeit von der Größenordnung 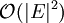$\mathcal{O}(|E|^2)$ hat. Effizienter ist der Algorithmus von Hierholzer, der einen Eulerkreis in Linearzeit berechnet. Er basiert darauf, dass sich ein eulerscher Graph in paarweise kantendisjunkte Kreise zerlegen lässt.

Algorithmus von Fleury

Im Algorithmus von Fleury spielen Brückenkanten eine wichtige Rolle. Das sind Kanten, ohne die der Graph in zwei Zusammenhangskomponenten zerfallen würde.

Der Algorithmus fügt einer anfangs leeren Kantenfolge alle Kanten eines Graphen hinzu, sodass ein Eulerkreis entsteht.

1. Wähle einen beliebigen Knoten als aktuellen Knoten.
2. Wähle unter den unmarkierten, mit dem aktuellen Knoten inzidenten Kanten eine beliebige Kante aus. Dabei sind zuerst Kanten zu wählen, die keine Brückenkanten sind.
3. Markiere die gewählte Kante und füge sie der Kantenfolge hinzu.
4. Wähle den anderen Knoten der gewählten Kante als neuen aktuellen Knoten.
5. Wenn noch unmarkierte Kanten existieren, dann gehe zu Schritt 2.

Ob eine Kante eine Brückenkante ist, kann mittels Tiefensuche in Laufzeit 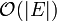$\mathcal{O}(|E|)$ überprüft werden. Da pro Schritt eine Kante entfernt wird, benötigen wir 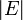$\left| E \right|$ Iterationen. Die Anzahl der pro Iteration geprüften Kanten entspricht dem Grad des aktuellen Knotens. Insgesamt kann man die gesamte Anzahl überprüfter Kanten durch 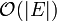$\mathcal{O}(|E|)$ beschränken. Die gesamte Laufzeit ist damit von der Größenordnung $\mathcal{O}(|E|^2)$.

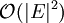Anwendungsbeispiele

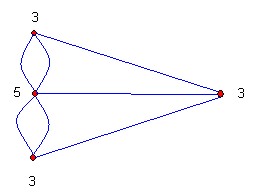
Das Königsberger Brückenproblem

Das Königsberger Brückenproblem lässt sich in folgendem Graphen ausdrücken:

Die roten Punkte (Knoten) sind die jeweiligen Stadtteile bzw. Standpunkte. Die blauen Linien (Kanten) sind die Brücken. Durch Probieren wird man herausfinden, dass es nicht möglich ist, alle Stadtteile hintereinander zu besuchen und jede Brücke nur ein einziges Mal zu benutzen. Es gibt also keinen Eulerweg und demzufolge auch keinen Eulerkreis. Warum ist das so?

Euler hat die folgende Gesetzmäßigkeit entdeckt: Wenn in einem Graphen G ein Eulerweg existiert, dann haben maximal 2 Knoten ungeraden Grad (also haben nicht mehr als zwei Knoten eine ungerade Anzahl angeschlossener Kanten). Beim Königsberger Brückengraphen gibt es vier Knoten mit ungeradem Grad (die Zahlen neben den Knoten geben hier deren Grad an). Deshalb ist der Stadtrundgang mit dem nur einmaligen Benutzen jeder Brücke unmöglich.

Ein ungerader Knoten ist entweder Anfang oder Ende des Weges über die Brücken: null ungerade Knoten würde bedeuten, dass Anfang und Ende des Weges in Königsberg identisch sind. Ein Weg mit Anfang und Ende hätte maximal zwei ungerade Knoten. Ergo ist es in Königsberg nicht möglich gewesen, alle Brücken in einem Wege nur jeweils einmal zu begehen.

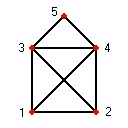
"Das-ist-das-Haus-vom-Nikolaus"

Das beliebte Kinderrätsel "Das ist das Haus vom Nikolaus" hingegen enthält einen Eulerweg, aber keinen Eulerkreis, da sein Graph zwei Knoten vom Grad 3 enthält.

Ein Eulerweg ist z.B. 1-2-4-3-1-4-5-3-2. Knoten 1 und 2 haben jeweils 3 Nachbarn, ihr Grad ist ungerade.

Ein Quadrat mit Diagonalen enthält keinen Eulerweg, da alle seine Knoten den Grad 3 haben. (Im Bild sind das nur die Punkte 1,2,3,4 mit den verbindenden Kanten.)

Literatur

• Wladimir Velminski: Leonhard Euler. Die Geburt der Graphentheorie. Kulturverlag Kadmos, Berlin 2008, ISBN 978-3-86599-056-3.
• Reinhard Diestel: Graphentheorie. 3. Auflage. Springer, 2006, ISBN 3-540-21391-0, S. 23–24

Siehe auch

• Wege, Pfade, Zyklen und Kreise in Graphen
• Hamiltonkreisproblem - ähnliches Problem, bei dem alle Knoten statt Kanten genau einmal durchlaufen werden müssen