Leonard Euler

Leonhard Euler

Leonhard Euler, Pastell von Emanuel Handmann, 1753 (Kunstmuseum Basel)

Gedenktafel am Haus Behrenstraße 21/22 in Berlin-Mitte

Grab Eulers auf dem Friedhof des Alexander-Nevskij-Klosters in Petersburg

Leonhard Euler auf dem Schweizerischen 10-Franken-Schein – Banknoten Serie von 1984

Leonhard Euler (* 15. April 1707 in Basel; † 18. September 1783 in Sankt Petersburg) war einer der bedeutendsten Mathematiker.

Leben

Euler wurde als der älteste Sohn des Pfarrers Paul Euler und Margarethe Bruckner geboren. Er besuchte das Gymnasium am Münsterplatz und nahm gleichzeitig Privatunterricht beim Mathematiker Johannes Burckhardt. Ab 1720 studierte er an der Universität Basel und hörte hier Vorlesungen von Johann Bernoulli. 1723 erlangte er durch einen Vergleich der Newtonschen und Kartesischen Philosophie in lateinischer Sprache die Magisterwürde. Seinen Plan, auch Theologie zu studieren, gab er 1725 auf. Am 17. Mai 1727 berief ihn Daniel Bernoulli an die Universität Sankt Petersburg. Er erbte die Professur des 1726 verstorbenen Nikolaus II. Bernoulli. Hier traf er auf Christian Goldbach. 1730 erhielt Euler die Professur für Physik und trat schließlich 1733 die Nachfolge von Daniel Bernoulli als Professor für Mathematik an. Er bekam in den folgenden Jahren immer stärkere Probleme mit seinem Augenlicht und war ab 1740 halbseitig blind.

1741 wurde er von Friedrich dem Großen an die Königlich-Preußische Akademie der Wissenschaften berufen. Euler korrespondierte und verglich seine Theorien weiterhin mit Christian Goldbach. Nach 25 Jahren in Berlin kehrte er 1766 zurück nach St. Petersburg. An seine Tätigkeit und sein damaliges Wohnhaus in Berlin erinnert eine Gedenktafel an der Behrenstraße 22/23, das heutige Haus der Bayerischen Landesvertretung in Berlin. Im St. Petersburg der Zarin Katharina der Großen wurde ihm an der Kaiserlich-russischen Akademie der Wissenschaften ein ehrenvoller Empfang bereitet. Er arbeitete wie in der ersten Sankt Petersburger Periode in der Kunstkammer und lebte in einem von Katharina der Großen geschenkten Palais mit seinem Sohn Johann Albrecht direkt an der Newa.

1771 erblindete er vollständig. Trotzdem entstand fast die Hälfte seines Lebenswerks in der zweiten Petersburger Zeit. Hilfe erhielt er dabei von seinen Söhnen Johann Albrecht, Karl und Christoph und seinem Sekretär Nikolaus Fuß, der nach seinem Tod als erster eine Würdigung verfasste. 1783 starb er an einer Hirnblutung. Trotz seiner Forderung wurde er nie Präsident der Universität, dieses Amt besetzte meist einer der Liebhaber Katharinas, aber sein Einfluss in der Universität war fast dem des Präsidenten ebenbürtig.

Da Euler und Friedrich der Große sich im Streit trennten, befinden sich heute neben den originalen Dokumenten aus der ersten und der zweiten Petersburger Periode auch die Dokumente aus der Berliner Zeit im Archiv in Sankt Petersburg.

Von ca. 1976 bis 1995 war Leonhard Euler auf der Schweizer 10-Franken-Note abgebildet. Zum 300. Geburtstag hat die Schweizerische Post 2007 eine Sondermarke herausgegeben.

Leistungen

Euler war extrem produktiv: Insgesamt gibt es 866 Publikationen von ihm. Ein großer Teil der heutigen mathematischen Symbolik geht auf Euler zurück (z. B. e, π, i, Summenzeichen ∑, f(x) als Darstellung für eine Funktion). 1744 gab er ein Lehrbuch der Variationsrechnung heraus. Euler kann auch als der eigentliche Begründer der Analysis angesehen werden. 1748 publizierte er das Grundlagenwerk Introductio in analysin infinitorum, in dem zum ersten Mal der Begriff der Funktion die zentrale Rolle spielt. Am 3. September 1750 las Leonhard Euler vor der Berliner Akademie der Wissenschaften ein Mémoire, in dem er erneut das von Isaac Newtons deklarierte Prinzip Kraft gleich Masse mal Beschleunigung vorstellte.

In den Werken Institutiones calculi differentialis (1765) und Institutiones calculi integralis (1768–1770) beschäftigte er sich außer mit der Differential- und Integralrechnung unter anderem mit Differenzengleichungen, elliptischen Integralen sowie auch mit der Theorie der Gamma- und Betafunktion. Andere Arbeiten setzen sich mit Zahlentheorie, Algebra (z. B. Vollständige Anleitung zur Algebra, 1770), angewandter Mathematik (z. B. Mechanica, sive motus scientia analytica exposita, 1736 und Theoria motus corporum solidorum seu rigidorum, 1765) und sogar mit der Anwendung mathematischer Methoden in den Sozial- und Wirtschaftswissenschaften auseinander (z. B. Rentenrechnung, Lotterien, Lebenserwartung).

In der Mechanik arbeitete er auf den Gebieten der Hydrodynamik (eulersche Bewegungsgleichung, Turbinengleichung) und der Kreiseltheorie (eulersche Kreiselgleichungen). Die erste analytische Beschreibung der Knickung eines mit einer Druckkraft belasteten Stabes geht auf Euler zurück; er begründete damit die Stabilitätstheorie. In der Optik veröffentlichte er Werke zur Wellentheorie des Lichts und zur Berechnung von optischen Linsen zur Vermeidung von Farbfehlern.

Seine 1736 veröffentlichte Arbeit Solutio problematis ad geometriam situs pertinentis beschäftigt sich mit dem Königsberger Brückenproblem und gilt als eine der ersten Arbeiten auf dem Gebiet der Graphentheorie.

Über seinen wenig rezipierten Beitrag zur mathematischen Musiktheorie (Tentamen novae theoriae musicae, 1739) bemerkte ein Biograph: „für die Musiker zu anspruchsvolle Mathematik, für die Mathematiker zu musikalisch.“

1745 übersetzte Leonhard Euler das Werk des Engländers Benjamin Robins „New principles of gunnery“ ins Deutsche, das im selben Jahre in Berlin unter dem Titel „Neue Grundsätze der Artillerie – enthaltend die Bestimmungen der Gewalt des Pulvers nebst einer Untersuchung über den Unterschied des Widerstands der Luft in schnellen und langsamen Bewegungen aus dem Englischen des Herrn Benjamin Robins übersetzt und mit den nötigen Erläuterungen und vielen Anmerkungen versehen“. Das Buch beschäftigt sich mit der sogenannten inneren Ballistik und – als Hauptthema – mit der äußeren Ballistik.
Seit Galilei hatten die Artilleristen die Flugbahn der Geschosse als Parabeln angesehen, indem sie den Luftwiderstand wegen der „Dünnheit“ der Luft glaubten vernachlässigen zu dürfen. Robins hat als einer der ersten wertvolle Experimente ausgeführt und gezeigt, dass dem nicht so ist; dass im Gegenteil die Flugbahn durch den Einfluss des Luftwiderstandes wesentlich abgeändert werde. Somit wurde dank Robins und Eulers Mithilfe „das erste Lehrbuch der Ballistik“ geschaffen. Da solch ein Lehrbuch einer Armee einen Vorteil verschaffte, wurde es 1777 wieder ins Englische und 1783 ins Französische übersetzt. In Frankreich wurde es sogar als offizielles Lehrbuch in den Militärschulen eingeführt, sodass sogar Napoléon Bonaparte es (als Leutnant) studieren musste.

Besondere Bedeutung in der breiten Öffentlichkeit erlangte seine populärwissenschaftliche Schrift Lettres à une princesse d’Allemagne von 1768, in der er in Form von Briefen an die Prinzessin von Anhalt-Dessau, eine Nichte Friedrichs des Großen, die Grundzüge der Physik, der Astronomie, der Mathematik, der Philosophie und der Theologie vermittelt.

Zeitgenossen Eulers waren unter anderen Christian Goldbach, Jean Baptiste le Rond d’Alembert, Alexis-Claude Clairaut, Johann Heinrich Lambert und einige Mitglieder der Familie Bernoulli.

Der deutsche Mathematiker Ferdinand Rudio (1856–1929) initiierte die Herausgabe von Eulers sämtlichen Werken. Zu Lebzeiten Rudios wurden mehr als 30 Bände publiziert. Bis heute wurden über 70 Bände herausgegeben.

Schriften

DDR-Briefmarke anlässlich des 200. Todestages Eulers (1983)

Sowjetische Briefmarke anlässlich des 250. Geburtstages Eulers (1957)

Der schwedische Mathematiker Gustaf Eneström hat ein chronologisches Verzeichnis der Publikationen Eulers erstellt. Eulers Schriften werden üblicherweise durch ihre Eneström-Nummer (E001–E866) referenziert.

Im Text erwähnte Publikationen:

• Mechanica sive motus scientia analytice exposita (1736, 2 Bände, E015, E016)
• Tentamen novae theoriae musicae (1739, E033)
• Solutio problematis ad geometriam situs pertinentis (1741, E053)
• Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes sive solutio problematis isoperimetrici latissimo sensu accepti (1744, E065)
• Introductio in analysin infinitorum (1748, 2 Bände, E101, E102)
• Découverte d’un nouveau principe de Mécanique, Mem. Acad. Roy. Sci. Berlin vol. 6, 1750 (1752), pp. 185–217.
• Institutiones calculi differentialis (1755, 2 Bände, E212)
• Theoria motus corporum solidorum seu rigidorum (1765, E289)
• Lettres à une princesse d'Allemagne (1768, 3 Bände, E343, E344, E417)
• Institutiones calculi integralis (1768–1770, 3 Bände, E342, E366, E385)
• Vollständige Anleitung zur Algebra (1770, 2 Bände, E387, E388)

Nach Euler Benanntes

• Euler-Bernoulli-Gleichung, Differentialgleichung vierter Ordnung, die der Kontinuumsmechanik des Balkens zugrunde liegt
• Euler-Charakteristik, in der Topologie eine Kennzahl für geschlossene Flächen
• eulersche Differentialgleichung, lineare gewöhnliche Differentialgleichung beliebiger Ordnung
• eulersches Dreieck, s. u.: „eulersches Kugeldreieck“
• Euler-Eytelwein-Formel, Formel für Seilhaftung
• Satz von Euler-Fermat (Zahlentheorie)
• eulersche Formel (Flächenkrümmung)
• eulersche Formeln (harmonische Analyse)
• eulersche Gerade: die Verbindungsgerade von Schwerpunkt, Höhenschnittpunkt und Umkreismittelpunkt eines Dreiecks
• Satz von Euler (Geometrie)
• Euler-Gleichungen (eulersche Bewegungsgleichungen), Grundgleichungen der Hydrodynamik idealer (reibungsfreier) Flüssigkeiten (Strömungsmechanik)
• eulersche Gleichungen (Kreiseltheorie), eulersche Kreiselgleichungen
• Euler-Hierholzer-Satz
• eulersche Identität e^iπ = − 1, ein Spezialfall der eulerschen Relation: $e^{iz} = \cos z + i\sin z\$
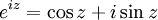
• eulersches Integral erster und zweiter Gattung
• eulersche Konstante siehe Euler-Mascheroni-Konstante (nicht zu verwechseln mit der eulerschen Zahl).
• eulersches Kugeldreieck, eine besondere Form des Kugeldreiecks
• Euler-Lagrange-Gleichung
• eulersche Last in der Balkentheorie die minimale axiale Last, die nötig ist, um eine Verbiegung zu bewirken
• eulersche Linie (auch „Eulertour“ oder „Eulerkreis“) in der Graphentheorie: ein Kantenzug, der jede Kante eines Graphen enthält
• Euler-Maclaurin-Formel
• Euler-Mascheroni-Konstante γ = 0.5772...
• Euler-Maruyama-Verfahren zur Lösung von stochastischen Differentialgleichungen
• eulersche φ-Funktion in der Zahlentheorie: φ(m) = Anzahl der zu m teilerfremden ganzen Zahlen a mit 0 < a < m
• eulerscher Polyedersatz
• eulersches Polygonzugverfahren (Integrationsverfahren für Differenzialgleichungen)
• Euler-Produkt, siehe Dirichletreihe
• eulersche Pseudoprimzahl
• eulersche Reihentransformation
• eulersche Turbinengleichung als Grundlage für die Kraftmaschine der modernen Stromerzeugung
• eulersche Vermutung, Vermutung der Zahlentheorie und Verallgemeinerung der fermatschen Vermutung
• die Euler-Wiege, eine kardanische Aufhängung, die in allen drei eulerschen Winkeln drehbar ist
• Euler-Wind
• eulersche Winkel
• eulersche Zahl e = exp(1) = 2,71828...
• eulersche Zahlen, verwandt mit den Bernoulli-Zahlen, treten als Taylor-Koeffizienten von sec(x) auf
• Euler-Zahlen bilden das dem Pascalschen Dreieck ähnliche Euler-Dreieck in der Kombinatorik
• Euler-Zahl ist eine dimensionslose Kennzahl in der Strömungsmechanik

Weiterhin sind zu seinen Ehren ein Mondkrater (der Krater Euler) und der Asteroid Euler (2002) benannt. Auch ein Programm für numerische und symbolische Berechnungen trägt seinen Namen.

Siehe auch

• Pentagonalzahlensatz von Leonhard Euler
• Lateinisches Quadrat und lateinisch-griechisches Quadrat von Leonhard Euler
• Sudoku

Literatur

• Gustaf Eneström: Verzeichnis der Schriften Leonhard Eulers. In: Jahresbericht der Deutschen Mathematiker-Vereinigung. Teubner, Leipzig 1913. ISSN 0012-0456
• Emil A. Fellmann: Leonhard Euler. Rowohlt, Reinbek 1995, ISBN 3-499-50387-5.
• Peter Mäder: Mathematik hat Geschichte. Metzler, Hannover 1992, 2000, ISBN 3-507-03363-1, S. 74–104
• Rüdiger Thiele: Leonhard Euler. BSB B.G.Teubner, Leipzig 1982, ISBN 3-322-00576-3 bzw. 978-3-322-00576-2.
• Rüdiger Thiele: The Mathematics and Science of Leonhard Euler (1707-1783). In: Glen van Brummelen / Michael Kinyon (Eds.): Mathematics and the Historian's Craft. Springer, New York, 2005, ISBN 978-0-387-25284-1, Kapitel 5, S. 81–140
• Leonhard Euler 1707−1783. Beiträge zu Leben und Werk. Gedenkband des Kantons Basel-Stadt. Birkhäuser, Basel 1983, ISBN 3-7643-1343-9.
• Wladimir Velminski: Leonhard Euler. Die Geburt der Graphentheorie. Kulturverlag Kadmos, Berlin 2008, ISBN 3-86599-056-8.

Weblinks

• WDR-Reportage zum 225. Todestag Eulers

Über Euler

• Artikel Leonhard Euler im Historischen Lexikon der Schweiz
• http://www.leonhard-euler.ch – Euler-Kommission der Schweizer Akademie der Wissenschaften
• Euler 2007
• Rubrik bei MAA von Ed Sandifer „How Euler did it“
• Biographie St.Andrews University
• Literatur von und über Leonhard Euler im Katalog der Deutschen Nationalbibliothek (Datensatz zu Leonhard Euler • PICA-Datensatz • Einträge im Musikarchiv)
• Genealogie Leonhard Eulers
• 300 Jahre Leonhard Euler (Berlin-Brandenburgische Akademie der Wissenschaften)
• Informationen aus „Beihefte zur Zeitschrift „Elemente der Mathematik““ von Ernst L. Locher
• Mathematischer Kalender in Spektrum der Wissenschaft
• verschiedene Aufsätze zu Euler in den BAMS 2007

Von Euler

• Gesammelte Schriften im Euler-Archiv (englische Benutzerführung)
• Eulers Schriften im Online-Angebot des Göttinger Digitalisierungszentrums
• Einleitung in die Analysis des Unendlichen (Deutsche Übersetzung)
• Digitalisierte Schriften zu Eulers Wirken in Berlin (BBAW)
• Digitalisierte Werke von Euler – SICD der Universitäten von Strasbourg
• Briefwechsel mit Friedrich dem Großen – Digitale Ausgabe der Universitätsbibliothek Trier

Personendaten
NAME	Euler, Leonhard
KURZBESCHREIBUNG	Schweizer Mathematiker
GEBURTSDATUM	15. April 1707
GEBURTSORT	Basel
STERBEDATUM	18. September 1783
STERBEORT	Sankt Petersburg