- Ewald-Kugel
-
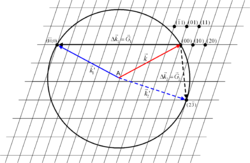
Mit Hilfe der Ewald-Kugel (benannt nach Paul Peter Ewald) lässt sich die Laue-Bedingung für konstruktive Interferenz bei der Streuung an einem Kristall anschaulich darstellen.
Die Kugel wird wie folgt konstruiert (vgl. die Abbildung): Man zeichnet die Punkte des reziproken Gitters des Kristalls auf (in der Abbildung ist ein zweidimensionaler Schnitt gezeigt). In dieses Netz wird nun der Wellenzahlvektor
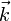 der einfallenden Welle so eingezeichnet, dass er am Gitterpunkt (00) endet. Der Anfangspunkt von
der einfallenden Welle so eingezeichnet, dass er am Gitterpunkt (00) endet. Der Anfangspunkt von 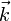 sei A. Dieser fällt i.A. nicht mit einem Gitterpunkt zusammen. Um A wird nun eine Kugel (in der Abbildung ein Kreis!) mit dem Radius
sei A. Dieser fällt i.A. nicht mit einem Gitterpunkt zusammen. Um A wird nun eine Kugel (in der Abbildung ein Kreis!) mit dem Radius 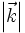 eingezeichnet. Bei der elastischen Streuung gilt
eingezeichnet. Bei der elastischen Streuung gilt 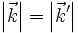 (d.h. dass sich bei der Streuung nur die Richtung des einfallenden Strahls ändert, nicht jedoch der Betrag des Wellenvektors). Das bedeutet nun, dass alle Wellenvektoren der gebeugten Wellen von A ausgehend ebenfalls auf der Kugeloberfläche enden. Notwendige Voraussetzung für das Auftreten eines Beugungsmaximums ist aber nun, dass die Laue-Bedingung
(d.h. dass sich bei der Streuung nur die Richtung des einfallenden Strahls ändert, nicht jedoch der Betrag des Wellenvektors). Das bedeutet nun, dass alle Wellenvektoren der gebeugten Wellen von A ausgehend ebenfalls auf der Kugeloberfläche enden. Notwendige Voraussetzung für das Auftreten eines Beugungsmaximums ist aber nun, dass die Laue-Bedingung 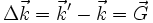 erfüllt ist. Dies ist genau für die abgebeugten Wellenvektoren
erfüllt ist. Dies ist genau für die abgebeugten Wellenvektoren 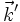 der Fall, die von A ausgehend auf Punkte des reziproken Gitters zeigen (also die Gitterpunkte die von der Oberfläche der Ewald-Kugel geschnitten werden). In der Abbildung ist dies für zwei Wellenvektoren (
der Fall, die von A ausgehend auf Punkte des reziproken Gitters zeigen (also die Gitterpunkte die von der Oberfläche der Ewald-Kugel geschnitten werden). In der Abbildung ist dies für zwei Wellenvektoren (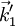 mit zugehörigem reziproken Gittervektor
mit zugehörigem reziproken Gittervektor 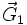 sowie
sowie 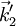 mit zugehörigem reziproken Gittervektor
mit zugehörigem reziproken Gittervektor 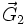 ) illustriert.
) illustriert.An dieser Konstruktion wird auch anschaulich klar, warum bei großen Wellenlängen λ (d.h. kleine Wellenzahl k) keine Beugung am Kristall stattfinden kann: Es gibt keine möglichen Vektoren
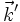 mehr, die die Laue-Bedingung erfüllen können, da die Ewald-Kugel zu klein wird.
mehr, die die Laue-Bedingung erfüllen können, da die Ewald-Kugel zu klein wird.Siehe auch: Röntgenbeugung, Elektronenbeugung.
Wikimedia Foundation.