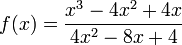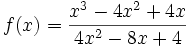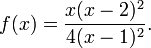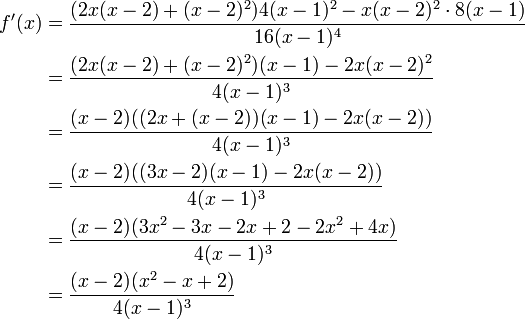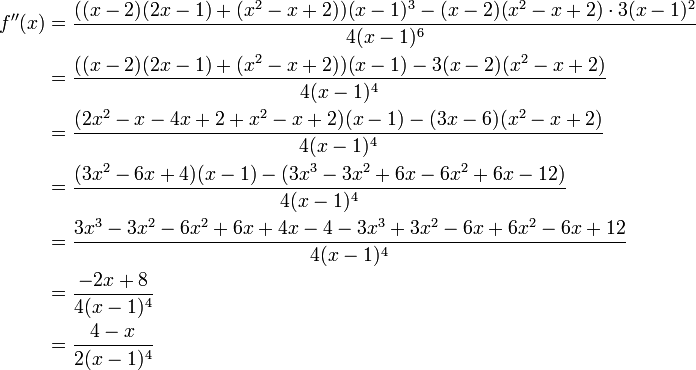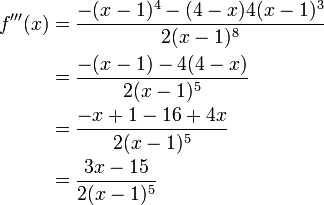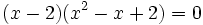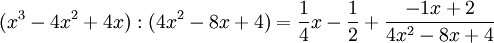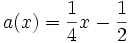- Extremwertproblem
-
Unter Kurvendiskussion versteht man in der Mathematik die Untersuchung des Graphen einer Funktion auf dessen Eigenschaften, wie zum Beispiel Nullstellen, Hoch- und Tiefpunkte, Wendepunkte, Polstellen, Verhalten im Unendlichen usw. Die Ergebnisse einer solchen Kurvendiskussion erleichtern die Anfertigung einer Skizze des Graphen.
Definitionsbereich
Bei einer Kurvendiskussion wird fast immer die Menge
 aller reellen Zahlen als Grundmenge vorausgesetzt. Der maximale Definitionsbereich einer Funktion f ist also die Menge aller reellen Zahlen x, für die der Funktionswert f(x) definiert ist. Für ganzrationale Funktionen (Polynomfunktionen) ist der maximale Definitionsbereich gleich
aller reellen Zahlen als Grundmenge vorausgesetzt. Der maximale Definitionsbereich einer Funktion f ist also die Menge aller reellen Zahlen x, für die der Funktionswert f(x) definiert ist. Für ganzrationale Funktionen (Polynomfunktionen) ist der maximale Definitionsbereich gleich  . Bei gebrochenrationalen Funktionen gehören alle reellen Zahlen mit Ausnahme derer, für die der Nenner Nullstellen aufweist, zum maximalen Definitionsbereich.
. Bei gebrochenrationalen Funktionen gehören alle reellen Zahlen mit Ausnahme derer, für die der Nenner Nullstellen aufweist, zum maximalen Definitionsbereich.Beispiele:
Der Nenner des Bruchs darf nicht gleich 0 sein. Daher sind die x-Werte 0 und 3 ausgeschlossen.
Der Radikand, also der Rechenausdruck unter der Quadratwurzel, muss größer oder gleich 0 sein. Diese Bedingung ist genau für die Zahlen erfüllt, deren Betrag kleiner oder gleich 5 ist.
Die natürliche Logarithmusfunktion ln ist nur für positive Argumente definiert. Also muss x > − 4 gelten.
Schnittpunkte mit den Koordinatenachsen
Um die Nullstellen einer Funktion f und damit die Schnittpunkte des Funktionsgraphen mit der x-Achse zu finden, wird die Lösungsmenge der Gleichung f(x) = 0 berechnet. Die genaue Vorgehensweise hängt davon ab, welche Funktion untersucht wird. Ist die Funktion f beispielsweise durch einen Bruchterm gegeben, so wird der Zähler gleich 0 gesetzt, um die Nullstellen zu erhalten.
Um den Schnittpunkt des Funktionsgraphen mit der y-Achse zu bestimmen, wird für x der Wert 0 eingesetzt. Der Y-Achsenabschnitt liegt dann folglich bei (0 | f(0)).
Symmetrieeigenschaften
Bei der Beantwortung der Frage, ob der Graph der gegebenen Funktion in irgendeiner Weise symmetrisch ist, müssen mehrere Fälle berücksichtigt werden.
Achsensymmetrie bezüglich der y-Achse
- Der Graph einer Funktion f ist genau dann achsensymmetrisch bezüglich der y-Achse, wenn für beliebige x-Werte des Definitionsbereiches gilt:
- f( − x) = f(x)
Bei ganzrationalen Funktionen bedeutet diese Bedingung, dass nur gerade Exponenten auftreten.
Punktsymmetrie bezüglich des Ursprungs
- Der Graph einer Funktion f ist genau dann punktsymmetrisch bezüglich des Ursprungs, wenn für beliebige x-Werte des Definitionsbereiches gilt:
- f( − x) = − f(x)
Der Graph einer ganzrationalen Funktion ist genau dann punktsymmetrisch bezüglich des Ursprungs, wenn nur ungerade Exponenten vorkommen.
Achsensymmetrie bezüglich einer beliebigen Achse
- Achsensymmetrie in Bezug auf die Gerade mit der Gleichung x = x0 (parallel zur y-Achse) lässt sich überprüfen mithilfe der Bedingung
- f(x0 − h) = f(x0 + h).
Achsensymmetrisch sind unter anderem die Graphen der quadratischen Funktionen. Die Symmetrieachse ergibt sich in diesem Fall aus der x-Koordinate des (Parabel-)Scheitels.
Punktsymmetrie bezüglich eines beliebigen Zentrums
- Die Bedingung für Punktsymmetrie bezüglich des Punktes (x0 | y0) lautet
- f(x0 − h) + f(x0 + h) = 2y0
oder (äquivalent)
- f(x0 + h) − y0 = y0 − f(x0 − h).
Die Graphen aller kubischen Funktionen sind punktsymmetrisch. Symmetriezentrum ist jeweils der (einzige) Wendepunkt (siehe unten).
Extrempunkte
Um die Extrempunkte - das heißt Hoch- und Tiefpunkte - einer stetig differenzierbaren Funktion f zu bestimmen, wird die erste Ableitung von f gleich 0 gesetzt, das heißt, die Lösungsmenge der Gleichung
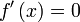 wird berechnet. Alle Lösungen dieser Gleichung sind mögliche Extremstellen.
wird berechnet. Alle Lösungen dieser Gleichung sind mögliche Extremstellen.Die Bedingung
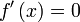 ist allerdings nur eine notwendige Bedingung für Extremstellen. Eine Stelle mit der Steigung 0 könnte auch ein Sattelpunkt sein. Das Standardbeispiel ist f(x) = x3 an der Stelle 0. Obwohl
ist allerdings nur eine notwendige Bedingung für Extremstellen. Eine Stelle mit der Steigung 0 könnte auch ein Sattelpunkt sein. Das Standardbeispiel ist f(x) = x3 an der Stelle 0. Obwohl 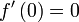 gilt, ist der Punkt (0 | 0) kein Extrempunkt, sondern ein Sattelpunkt.
gilt, ist der Punkt (0 | 0) kein Extrempunkt, sondern ein Sattelpunkt.Zum Nachweis der Extrempunkteigenschaft benötigt man daher eine der weiter unten genannten hinreichenden Bedingungen.
Notwendige Bedingung
Es leuchtet anschaulich ein, dass die Tangente an einen Funktionsgraphen in einem Extrempunkt waagrecht verlaufen muss. Die Steigung einer solchen Tangente muss also den Wert 0 haben. Präziser gilt:
- f sei eine reelle Funktion, die auf einem offenen Intervall I definiert und an der Stelle x0 (mit
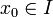 ) differenzierbar ist. Nimmt f an der Stelle x0 ein relatives Extremum (also ein relatives Maximum oder Minimum) an, so gilt
) differenzierbar ist. Nimmt f an der Stelle x0 ein relatives Extremum (also ein relatives Maximum oder Minimum) an, so gilt 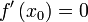 .
.
Am Rand des Definitionsbereichs und an Stellen, an denen die gegebene Funktion nicht differenzierbar ist, sind die Voraussetzungen dieser Bedingung nicht erfüllt. Relative Extrema an solchen Stellen lassen sich also im Allgemeinen nicht durch Nullsetzen der Ableitung bestimmen.
Hinreichende Bedingung: Wert der zweiten Ableitung
Die folgende hinreichende Bedingung bietet oft eine bequeme Möglichkeit, den Nachweis für ein relatives Extremum zu führen und zugleich die Art (Maximum oder Minimum) zu bestimmen. Da auch die zweite Ableitung benötigt wird, spricht man gelegentlich vom
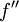 -Test.
-Test.- f sei eine reelle Funktion, die in einem offenen Intervall I definiert und zweimal differenzierbar ist.
Gilt an einer Stelle
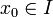 zugleich
zugleich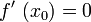 und
und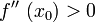 ,
,
so hat f an dieser Stelle ein relatives Minimum.
Gilt dagegen zugleich
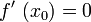 und
und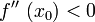 ,
,
so hat f an dieser Stelle ein relatives Maximum.
Beispiel:
Durch Nullsetzen der ersten Ableitung ( − 2x + 8 = 0) erhält man x = 4. Einsetzen in die zweite Ableitung ergibt
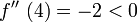 (Bedingung für ein relatives Maximum). Der Graph von f hat also genau einen Extrempunkt, nämlich einen Hochpunkt mit der x-Koordinate 4.
(Bedingung für ein relatives Maximum). Der Graph von f hat also genau einen Extrempunkt, nämlich einen Hochpunkt mit der x-Koordinate 4.Gelegentlich gilt sowohl
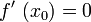 als auch
als auch 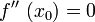 . In diesem Fall sind weitere Untersuchungen nötig, um zu entscheiden, ob eine Extremstelle vorliegt oder nicht. Das bedeutet konkret, dass solange abgeleitet werden muss, bis eine Ableitung gerader Ordnung - vierter, sechster,... Ordnung - vorliegt, die an dieser Stelle ungleich 0 ist.
. In diesem Fall sind weitere Untersuchungen nötig, um zu entscheiden, ob eine Extremstelle vorliegt oder nicht. Das bedeutet konkret, dass solange abgeleitet werden muss, bis eine Ableitung gerader Ordnung - vierter, sechster,... Ordnung - vorliegt, die an dieser Stelle ungleich 0 ist.Das einfachste Beispiel ist f(x) = x4. Die ersten drei Ableitungen an der Stelle x0 = 0, also
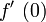 ,
, 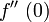 und
und 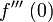 haben jeweils den Wert 0. Erst die vierte Ableitung f(4)(x) = 24 ermöglicht wegen
haben jeweils den Wert 0. Erst die vierte Ableitung f(4)(x) = 24 ermöglicht wegen 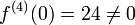 den Nachweis des Extremums. Das positive Vorzeichen lässt erkennen, dass sich an der Stelle x0 = 0 ein relatives Minimum befindet.
den Nachweis des Extremums. Das positive Vorzeichen lässt erkennen, dass sich an der Stelle x0 = 0 ein relatives Minimum befindet.In seltenen Fällen versagt auch dieses allgemeinere Kriterium, nämlich dann, wenn alle Ableitungen an der Stelle x0 gleich 0 sind.
Hinreichende Bedingung: Vorzeichen der ersten Ableitung
Ein weiteres Verfahren zum Nachweis der Extrempunkteigenschaft kommt ohne die Berechnung der zweiten Ableitung aus. Es wird untersucht, ob die erste Ableitung
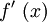 an der betrachteten Stelle x0 ihr Vorzeichen wechselt. Diese Methode, gelegentlich als VZW-Verfahren bezeichnet, lässt sich folgendermaßen anschaulich deuten:
an der betrachteten Stelle x0 ihr Vorzeichen wechselt. Diese Methode, gelegentlich als VZW-Verfahren bezeichnet, lässt sich folgendermaßen anschaulich deuten:Durchläuft man den Funktionsgraphen in der Umgebung eines Hochpunkts von links nach rechts, so lässt sich das Aussehen dieser Kurve wie folgt beschreiben:
- Links vom Hochpunkt steigt der Funktionsgraph an. Die Steigung ist positiv.
- Im Hochpunkt selbst verläuft die Tangente waagerecht. Die Steigung ist 0.
- Rechts vom Hochpunkt fällt der Funktionsgraph. Die Steigung ist negativ.
Entsprechendes, nur umgekehrt, gilt für Tiefpunkte.
- f sei eine reelle Funktion, die in einem offenen Intervall I definiert und differenzierbar ist.
Gilt an einer Stelle
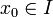 zugleich
zugleich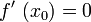 ,
,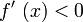 für
für 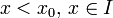 und
und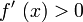 für
für 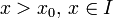 ,
,
so hat f an dieser Stelle ein relatives Minimum.
Gilt an einer Stelle
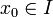 zugleich
zugleich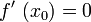 ,
,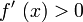 für
für 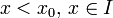 und
und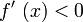 für
für 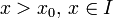 ,
,
so hat f an dieser Stelle ein relatives Maximum.
Beispiel:
Nullsetzen der Ableitung (4x3 = 0) liefert als Stelle mit waagerechter Tangente und damit als Kandidaten für eine Extremstelle x = 0. Beim VZW-Test betrachtet man x-Werte, die kleiner bzw. größer als 0 sind.
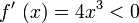 für x < 0
für x < 0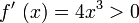 für x > 0
für x > 0
zeigt, dass ein Tiefpunkt vorliegt.
Ein Problem des VZW-Tests besteht darin, dass das Vorzeichen der Ableitung nicht nur für eine einzige Stelle ermittelt werden muss, sondern für ein ganzes Intervall. In der Schulmathematik bestimmt man daher oft nur für eine einzelne Stelle des Intervalls das Vorzeichen und schließt daraus, dass dieses Vorzeichen im ganzen Intervall gilt. Diese Vorgehensweise ist erlaubt, wenn die Funktion im Intervall I stetig differenzierbar ist.
Historische Randbemerkung: Die Bestimmung der Extrema aus der Tangentensteigung wurde erstmals von Fermat in einem Brief an Descartes vorgeschlagen - bevor es den Ableitungsbegriff gab.
Wendepunkte
Als Wendepunkte bezeichnet man diejenigen Punkte, in denen der gegebene Funktionsgraph zwischen Links- und Rechtskrümmung wechselt. Die Art der Krümmung lässt sich - unter gewissen Voraussetzungen - am Vorzeichen der zweiten Ableitung f ''(x) erkennen. Positives Vorzeichen lässt auf Linkskrümmung schließen, negatives Vorzeichen auf Rechtskrümmung. Beim Standardverfahren zur Bestimmung der Wendepunkte setzt man daher die zweite Ableitung gleich 0. Die Lösungen der Gleichung f ''(x) = 0 (siehe notwendige Bedingung) kommen als Wendestellen in Frage. Mit einer der unten aufgeführten hinreichenden Bedingungen weist man anschließend nach, dass tatsächlich ein Wendepunkt vorliegt.
Notwendige Bedingung
- f sei eine reelle Funktion, die in einem offenen Intervall I definiert und zweimal stetig differenzierbar ist. Hat der Graph von f an der Stelle
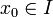 einen Wendepunkt, so gilt
einen Wendepunkt, so gilt
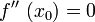 .
.
Hinreichende Bedingung: Wert der dritten Ableitung
Die zuletzt genannte Bedingung ist nicht hinreichend, sodass weitere Untersuchungen durchzuführen sind. Eine häufig zum Nachweis von Wendepunkten verwendete hinreichende Bedingung beruht auf der dritten Ableitung:
- f sei eine reelle Funktion, die in einem offenen Intervall I definiert und dreimal differenzierbar ist. Gilt an einer Stelle
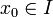 zugleich
zugleich
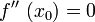 und
und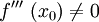 ,
,
so hat der Graph von f an der Stelle x0 eine Wendestelle.
Ist der Wert der dritten Ableitung an dieser Stelle größer als 0, so handelt es sich um eine Wendestelle mit Übergang in eine „Linkskrümmung“, ist er kleiner als 0, so handelt es sich um eine Wendestelle mit Übergang in eine „Rechtskrümmung“.
Hinreichende Bedingung: Vorzeichen der zweiten Ableitung
Ist an der Stelle x0 neben der zweiten Ableitung auch die dritte Ableitung gleich 0, so versagt das zuletzt genannte Kriterium. In diesem Fall untersucht man, ob die zweite Ableitung bei x0 das Vorzeichen wechselt.
- f sei eine reelle Funktion, die im offenen Intervall I definiert und zweimal differenzierbar ist. Gilt an der Stelle
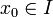 zugleich
zugleich
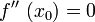 ,
,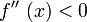 für x < x0,
für x < x0, 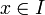 und
und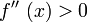 für x > x0,
für x > x0, 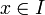
oder zugleich
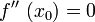 ,
,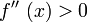 für x < x0,
für x < x0, 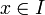 und
und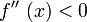 für x > x0,
für x > x0, 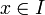 ,
,
so hat der Graph von f an der Stelle x0 eine Wendestelle.
Spezialfall: Sattelpunkte
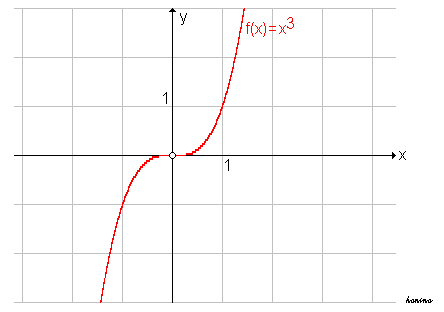
Einen Wendepunkt mit zugleich waagerechter Tangente nennt man einen Sattelpunkt oder Terrassenpunkt. Für ihn gilt demnach f '(x)=0 und f ''(x) = 0, wie im Beispiel der Funktion mit der Gleichung
- f(x) = x3
an der Stelle x = 0.
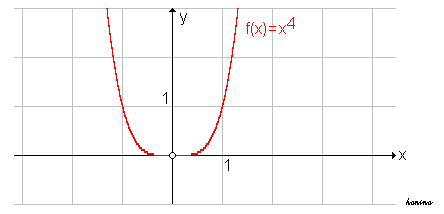
Allerdings ist das kein hinreichendes Kriterium, es kann auch f '(x)=0 und f ''(x) = 0 werden, ohne dass ein Sattelpunkt auftritt, wie im nachfolgenden Beispiel gezeigt wird:
- f(x) = x4
Erst wenn
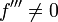 ist, ist ein Sattelpunkt erwiesen; allgemeiner gilt: Es liegt ein Wendepunkt vor, wenn der Grad der ersten von 0 verschiedenen Ableitung ungerade ist; ist der Grad gerade, so handelt es sich um ein Extremum.
ist, ist ein Sattelpunkt erwiesen; allgemeiner gilt: Es liegt ein Wendepunkt vor, wenn der Grad der ersten von 0 verschiedenen Ableitung ungerade ist; ist der Grad gerade, so handelt es sich um ein Extremum.Polstellen
Eine Polstelle liegt bei gebrochen-rationalen Funktionen genau dann an einer Stelle p vor, wenn das Nennerpolynom eine Nullstelle bei p hat und das Zählerpolynom eine Nullstelle einer niedrigeren Ordnung bei p oder keine Nullstelle bei p hat.
Haben sowohl das Zähler- als auch das Nennerpolynom bei p eine Nullstelle und ist die Ordnung der Nullstelle im Zählerpolynom nicht kleiner als die des Nennerpolynoms, handelt es sich um eine stetig hebbare Definitionslücke.
In der Hochschulmathematik gibt es noch weitere Arten von nicht definierten Stellen, die weder hebbare Lücken noch Polstellen sind.
Lücke
Im Falle von gebrochenrationalen Funktionen liegt an einer Stelle x0 eine stetig behebbare Definitionslücke vor, falls x0 nicht nur eine Nullstelle des Nenners, sondern auch eine Nullstelle des Zählers von mindestens gleich großem Grad ist. In diesem Fall lässt sich der zugehörige Linearfaktor (x − x0) herauskürzen.
Beispiel:
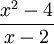 hat an der Stelle x = 2 eine hebbare Definitionslücke. Durch Kürzen des Faktors (x − 2) entsteht:
hat an der Stelle x = 2 eine hebbare Definitionslücke. Durch Kürzen des Faktors (x − 2) entsteht: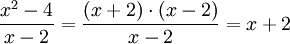 (für
(für 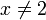 ).
).
Eine andere Möglichkeit zu testen, ob an der Stelle x0 eine stetig behebbare Definitionslücke vorliegt, besteht darin, den Grenzwert
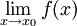 zu berechnen. Wenn dieser Limes existiert und endlich ist, liegt eine stetig behebbare Lücke vor.
zu berechnen. Wenn dieser Limes existiert und endlich ist, liegt eine stetig behebbare Lücke vor.Verhalten im Unendlichen
Um das Verhalten im Unendlichen herauszufinden, wird der Funktionswert der Funktion f(x) untersucht, wenn x über alle Grenzen wächst, also gegen ∞ geht:
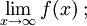
Entsprechendes für -∞.
Übersicht über Kriterien
Diskutiert wird 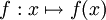
Untersuchungsaspekt Kriterium Nullstelle 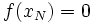
Extremstelle 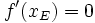
(notwendiges Kriterium) 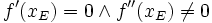
(hinreichendes Kriterium) Minimalstelle 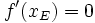
(notwendiges Kriterium) 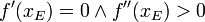
(hinreichendes Kriterium) Maximalstelle 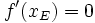
(notwendiges Kriterium) 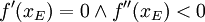
(hinreichendes Kriterium) Wendestelle 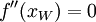
(notwendiges Kriterium) 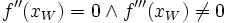
(hinreichendes Kriterium) Sattelstelle 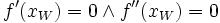
(notwendiges Kriterium) 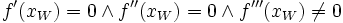
(hinreichendes Kriterium) Verhalten im Unendlichen 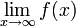 ,
,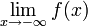
Symmetrie Achsensymmetrie zur Koordinatenachse 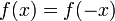
Punktsymmetrie zum Koordinatenursprung 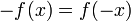
Monotonie steigend/streng steigend 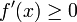
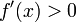
fallend/streng fallend 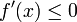
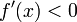
Krümmung Linkskrümmung/Konvexbogen (nach oben offen) 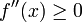
Rechtskrümmung/Konkavbogen (nach unten offen) 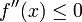
Periodizität 
Diskutiert wird 
Untersuchungsaspekt Kriterium Definitionsbereich 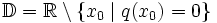
Polstelle 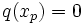
(notwendiges Kriterium) 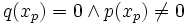
(hinreichendes Kriterium) Beispiel: Ganzrationale Funktion
Die zu untersuchende Funktion sei:
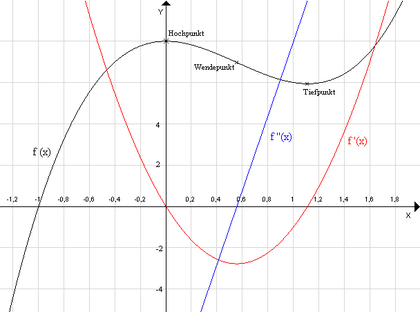
- f(x) = 3x3 − 5x2 + 8
Der Graph der Funktion f ist im Bild schwarz dargestellt, zudem sind die erste (rot) und zweite (blau) Ableitung eingetragen:
Nullstellen
Durch Ausprobieren (zum Beispiel durch Anfertigen einer Wertetabelle) oder gemäß der Folgerung mit dem Wissen nach Gauß, dass jede ganzzahlige Nullstelle Teiler des absoluten Gliedes 8 sein muss, lässt sich die Nullstelle x = − 1 finden. Gäbe es keine derart einfach erkennbare Nullstelle, so ließe sich die Formel von Cardano für Gleichungen 3. Grades oder das newtonsche Näherungsverfahren anwenden.
Zur Nullstelle x = − 1 gehört der Linearfaktor (x − ( − 1)) = (x + 1). Um die weiteren Nullstellen zu finden, wird eine Polynomdivision durch diesen Linearfaktor durchgeführt und das Ergebnis gleich 0 gesetzt. Etwas schneller erhält man das Ergebnis mit dem Horner-Schema. Auf diese Weise reduziert sich der Grad der Gleichung um 1.
- (3x3 − 5x2 + 8):(x + 1) = 3x2 − 8x + 8
Die neue Gleichung 3x2 − 8x + 8 = 0 hat keine Lösung. x = − 1 ist folglich die einzige reelle Nullstelle.
Extrempunkte
Die erste Ableitungsfunktion ist
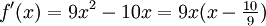 .
.
Diese besitzt Nullstellen bei x1 = 0 und bei
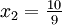 . Dies bedeutet, dass hier Extremstellen vorliegen können.
. Dies bedeutet, dass hier Extremstellen vorliegen können.Die zweite Ableitungsfunktion
hat an obigen Stellen die Funktionswerte
bzw.
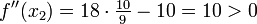 .
.
Daher hat der Funktionsgraph bei x1 einen Hochpunkt (erste Ableitung gleich 0, zweite Ableitung negativ) und bei x2 einen Tiefpunkt (erste Ableitung gleich 0, zweite Ableitung positiv). Die y-Koordinaten der beiden Extrempunkte ergeben sich durch Einsetzen der x-Koordinaten in f(x).
Wendepunkte
Zur Bestimmung der Wendestellen wird die zweite Ableitung f''(x) = 18x − 10 gleich null gesetzt:
- 18x − 10 = 0
Die einzige Lösung dieser Gleichung ist
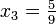 . Zur Bestätigung, dass tatsächlich ein Wendepunkt vorliegt, kann man die dritte Ableitung f'''(x) = 18 verwenden. Wegen
. Zur Bestätigung, dass tatsächlich ein Wendepunkt vorliegt, kann man die dritte Ableitung f'''(x) = 18 verwenden. Wegenist die Wendepunkteigenschaft gesichert. Die y-Koordinate des Wendepunkts ergibt sich zu
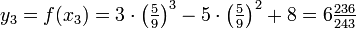 .
.
Polstellen und Verhalten im Unendlichen
Polstellen gibt es bei Polynomen nicht. Als Polynom ungeradzahliger Ordnung (höchster Exponent bei x3) geht die Funktion gegen +∞ bzw. -∞, wenn x gegen +∞ bzw. -∞ geht.
Beispiel: Gebrochen-rationale Funktion
Gegeben ist die Funktion mit der Gleichung
Definitionsbereich
Die Funktion ist nur dort definiert, wo der Nenner ungleich 0 ist. Die Untersuchung des Nenners auf Nullstellen ergibt:
- 4x2 − 8x + 4 = 0
- x2 − 2x + 1 = 0
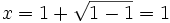 oder
oder 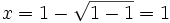
Die quadratische Gleichung hat eine doppelte Lösung bei x = 1. Nur bei x = 1 wird also der Nenner 0. Der Definitionsbereich ist folglich
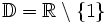 .
.
Menge der reellen Zahlen, ausgenommen die 1. Der Nenner kann - in Linearfaktoren zerlegt - als
- 4(x − 1)(x − 1) oder 4(x − 1)2
geschrieben werden.
Nullstellen
Die Bedingung für Nullstellen ist
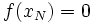 . Hierzu genügt es, dass der Zähler 0 wird, solange nicht zugleich der Nenner 0 wird. Untersuchung des Zählers auf Nullstellen ergibt:
. Hierzu genügt es, dass der Zähler 0 wird, solange nicht zugleich der Nenner 0 wird. Untersuchung des Zählers auf Nullstellen ergibt:- x3 − 4x2 + 4x = 0
- x(x2 − 4x + 4) = 0
- x = 0 oder
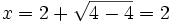 oder
oder 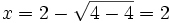
Der Zähler hat eine einfache Nullstelle bei x = 0 und eine doppelte bei x = 2. Beide Stellen liegen im Definitionsbereich. f(x) hat also die Nullstellen x1 = 0 sowie x2 = x3 = 2.
Der Zähler kann - in Linearfaktoren zerlegt - als
- x(x − 2)(x − 2) = x(x − 2)2
geschrieben werden.
Im Rahmen der Schulmathematik wird häufig darauf Wert gelegt, dass bei jedem x der Index N für „Nullstelle“ dazugeschrieben wird:
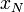 .
.Polstellen
An der Stelle x = 1 hat der Nenner eine zweifache Nullstelle, ohne dass zugleich der Zähler 0 wird. Es liegt also eine Polstelle bei x = 1 vor. Sollte der Zähler auch 0 werden, so muss für eine Polstelle die Ordnung der Nennernullstelle größer als die Ordnung der Zählernullstelle sein.
Sofern der Nenner einer gebrochenrationalen Funktion an einer Stelle x=a gleich 0 ist, ist die Funktion an dieser Stelle nicht definiert. Ist der Nenner gleich 0, der Zähler aber ungleich 0, so besitzt die Funktion an dieser Stelle einen Pol („Unendlichkeitsstelle“).
Symmetrie
Der Graph der Funktion wird an dieser Stelle auf Symmetrie untersucht. Oft erfolgt nur eine Untersuchung auf Achsensymmetrie zur y-Achse (Bedingung f( − x) = f(x)) und auf Punktsymmetrie zum Ursprung des Koordinatensystems (Bedingung f( − x) = − f(x)).
Im Beispiel wird in
x ersetzt durch − x. Nach dem Ausmultiplizieren entsteht
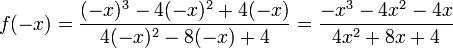 .
.
Da f( − x) weder mit f(x) noch mit − f(x) übereinstimmt, ist der Graph von f weder achsensymmetrisch zur y-Achse noch punktsymmetrisch zum Ursprung.
Etwas schwieriger gestaltet sich die Untersuchung auf Achsensymmetrie bezüglich einer beliebigen Achse beziehungsweise auf Punktsymmetrie bezüglich eines beliebigen Punktes. Wegen
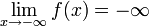 und
und 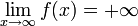 lässt sich Achsensymmetrie ausschließen. Als Symmetriezentrum (Punktsymmetrie) käme höchstens der Schnittpunkt der Asymptoten (siehe unten), also der Punkt
lässt sich Achsensymmetrie ausschließen. Als Symmetriezentrum (Punktsymmetrie) käme höchstens der Schnittpunkt der Asymptoten (siehe unten), also der Punkt 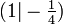 in Frage. Da aber beispielsweise die Punkte (0 | 0) und (2 | 0) nicht symmetrisch bezüglich
in Frage. Da aber beispielsweise die Punkte (0 | 0) und (2 | 0) nicht symmetrisch bezüglich 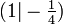 liegen, ist der Graph auch nicht punktsymmetrisch.
liegen, ist der Graph auch nicht punktsymmetrisch.Ableitungen
Zu bilden sind die Ableitungen von
Die Darstellung in Linearfaktoren ist zweckmäßiger, da sie das Ausklammern und Kürzen vereinfacht. Dies ergibt zunächst
für die erste Ableitung. Dann wird die zweite
und die dritte Ableitung
gebildet.
Extrempunkte
Hierfür muss
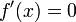 werden. Es genügt, die Nullstellen des Zählers zu untersuchen:
werden. Es genügt, die Nullstellen des Zählers zu untersuchen:hat die Lösung x = 2. Die zweite Klammer hat keine reellen Lösungen. x = 2 liegt im Definitionsbereich. Der Funktionswert an dieser Stelle ist
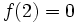 , da hier eine Nullstelle vorliegt. Die zweite Ableitung ist an dieser Stelle
, da hier eine Nullstelle vorliegt. Die zweite Ableitung ist an dieser Stelle 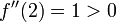 , es handelt sich also um einen Tiefpunkt bei (2/ 0).
, es handelt sich also um einen Tiefpunkt bei (2/ 0).Wendepunkte
Der Wendepunkt wird ermittelt, indem die zweite Ableitung gleich 0 gesetzt wird. Aus diesem Ansatz ergibt sich xW = 4. Einsetzen dieses Wertes in die dritte Ableitung ergibt
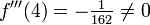 . Es liegt also tatsächlich ein Wendepunkt vor. Die Berechnung von f(4) ergibt schließlich die y-Koordinate
. Es liegt also tatsächlich ein Wendepunkt vor. Die Berechnung von f(4) ergibt schließlich die y-Koordinate 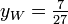 . Der gesuchte Wendepunkt ist somit
. Der gesuchte Wendepunkt ist somit 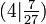 .
.Asymptoten
An der Polstelle, also bei x = 1, liegt eine senkrechte Asymptote. Da der Grad des Zählers (3) um 1 größer ist als der des Nenners (2), wird f(x) gegen
 gehen für x gegen
gehen für x gegen  . Die Differenz 3-2 = 1 gibt an, dass sich der Graph an eine lineare Funktion (Gerade) asymptotisch annähern wird. Die Geradengleichung folgt durch Polynomdivision:
. Die Differenz 3-2 = 1 gibt an, dass sich der Graph an eine lineare Funktion (Gerade) asymptotisch annähern wird. Die Geradengleichung folgt durch Polynomdivision:Für x gegen
 geht der letzte Term gegen 0. Die Gleichung der Asymptote ist also
geht der letzte Term gegen 0. Die Gleichung der Asymptote ist alsoAllgemein:
- Ist der Nennergrad größer als der Zählergrad, ist die Asymptote die x-Achse.
- Ist der Nennergrad gleich dem Zählergrad, ist die Asymptote eine Parallele zur x-Achse.
- Ist der Nennergrad um 1 kleiner als der Zählergrad, ist die Asymptote schräg.
- Ist der Nennergrad um mehr als 1 kleiner als der Zählergrad, ist die Asymptote keine Gerade, sondern kurvig.
Didaktische Fragen
In der Mathematikdidaktik wird seit spätestens den 90er Jahren diskutiert, inwieweit die Kurvendiskussion durch die Verfügbarkeit von grafikfähigen Taschenrechnern und dedizierter Software (Funktionenplotter) überholt ist.
Kritisiert wird, dass die Kurvendiskussion eine rein rechnerische Routine ist, die wenig Verständnis vermittelt. Andererseits ist sie gerade deshalb als relativ sicher vorzubereitendes Prüfungsthema bei schwächeren Schülern und Studenten vergleichsweise beliebt.
In den zentralen Abiturprüfungen hat es sich deshalb durchgesetzt, dass solch schematische Aufgaben nur sehr selten gestellt werden. Beliebter sind eingekleidete Aufgaben oder Aufgaben, in denen Zusammenhangswissen abgefragt wird, zum Beispiel über Zusammenhänge zwischen Ableitungsfunktion und Ausgangsfunktion.
Weblinks
Wikimedia Foundation.

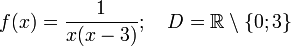
![f(x) = \sqrt{25-x^2}; \quad D = \{ x \in \R | -5 \le x \le 5 \} = [-5;5]](/pictures/dewiki/51/3b7fd32267537012dfe4177e8ac4ff1f.png)
![f(x) = \ln(x+4); \quad D = \{ x \in \R | x &amp;gt; -4 \} = ]-4;\infty[](/pictures/dewiki/48/0f9fb377d82e02e006d8cc68c6144929.png)
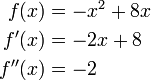
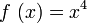
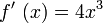
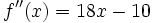
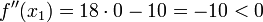
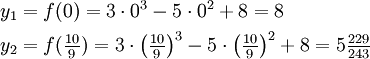
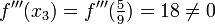
.PNG)