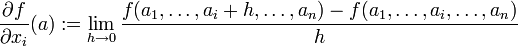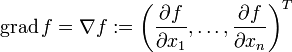- ∂
-
In der Differentialrechnung ist eine partielle Ableitung die Ableitung einer Funktion mit mehreren Argumenten nach einem dieser Argumente.
Inhaltsverzeichnis
Definition
Sei U eine offene Teilmenge des euklidischen Raums
 , und
, und 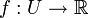 eine Funktion. Sei weiterhin ein Element
eine Funktion. Sei weiterhin ein Element  in U gegeben. Falls für die natürliche Zahl i mit
in U gegeben. Falls für die natürliche Zahl i mit 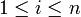 der folgende Grenzwert existiert:
der folgende Grenzwert existiert:dann nennt man ihn die partielle Ableitung von f nach der i-ten Variablen xi im Punkt a. Die Funktion f heißt dann im Punkt a partiell differenzierbar. Das Symbol
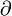 (der kursive Schnitt des kyrillischen Minuskel д) wird als d oder zur Unterscheidung auch del ausgesprochen.
(der kursive Schnitt des kyrillischen Minuskel д) wird als d oder zur Unterscheidung auch del ausgesprochen.Die partielle Ableitung nach xi ist selbst wieder eine Funktion von U nach
 , falls f in ganz U nach xi partiell differenzierbar ist.
, falls f in ganz U nach xi partiell differenzierbar ist.Den Vektor
nennt man den Gradienten von f. Das Symbol
 wird Nabla genannt. Als abkürzende Schreibweise ist auch oft
wird Nabla genannt. Als abkürzende Schreibweise ist auch oft 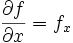 oder
oder 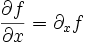 zu finden.
zu finden.Zusammenhang Ableitung, partielle Ableitung, Stetigkeit
- Total differenzierbare Funktionen sind stetig.
- Total differenzierbare Funktionen sind partiell differenzierbar.
- Stetig partiell differenzierbare Funktionen (das sind Funktionen, deren partielle Ableitungen stetig sind) sind stetig total differenzierbar (und umgekehrt).
- Partiell differenzierbare Funktionen sind i.A. nicht stetig und damit auch nicht total differenzierbar.
Verwendung
Partielle Ableitungen ermöglichen die Berechnung einer Lösung für Probleme, die von mehreren Parametern abhängen.
Das Bestimmen der optimalen Lösung ist ein Extremwertproblem. Einfache Extremwertprobleme findet man in der Analysis bei der Berechnung von Maxima und Minima einer Funktion einer reellen Variablen (vgl. hierzu den Artikel über Differentialrechnung).
Die Verallgemeinerung des Differentialquotienten auf Funktionen mehrerer Variablen (Veränderlichen, Parameter) ermöglicht die Bestimmung ihrer Extremwerte, und für die Berechnung werden partielle Ableitungen benötigt.
In der Differentialgeometrie benötigt man partielle Ableitungen zur Bestimmung eines totalen Differentials. Anwendungen für totale Differentiale findet man in großem Maße in der Thermodynamik.
Partielle Ableitungen sind darüber hinaus ein wesentlicher Bestandteil der Vektoranalysis. Sie bilden die Komponenten des Gradienten, des Laplace-Operators, der Divergenz und der Rotation in Skalar- und Vektorfeldern. Sie treten auch in der Jacobi-Matrix auf.
Beispiele
Beispiel 1
Als Beispiel wird die Funktion
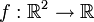 mit f(x,y): = x2 + y2 betrachtet, die von den beiden Variablen x und y abhängt.
mit f(x,y): = x2 + y2 betrachtet, die von den beiden Variablen x und y abhängt.Betrachtet man y als eine Konstante, z. B. y = 3, so hängt die Funktion
 mit g(x) = f(x,3) nur noch von der Variablen x ab:
mit g(x) = f(x,3) nur noch von der Variablen x ab:- f(x,3) = x2 + 9
Für die neue Funktion gilt folglich g(x) = x2 + 9 und man kann den Differenzialquotienten bilden
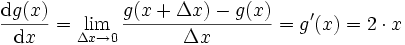
Das gleiche Ergebnis erhält man, wenn man die partielle Ableitung der Funktion f nach x bildet:
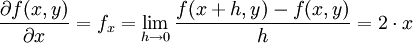
Die partielle Ableitung von f nach y lautet entsprechend:
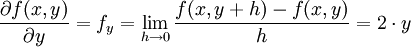
Dieses Beispiel demonstriert, wie die partielle Ableitung einer Funktion bestimmt wird, die von mehreren Variablen abhängt:
Bis auf eine Variable werden alle anderen Variablen als konstant angenommen, bezüglich dieser einen Variablen wird der Differenzialquotient bestimmt. Als Ergebnis erhält man die partielle Ableitung der Funktion nach dieser einen Variablen.
Beispiel 2
Das folgende Beispiel gibt eine geometrische Deutung der partiellen Ableitung:
In einem dreidimensionalen Koordinatensystem wird der Funktionsgraph der Funktion
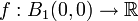 mit
mit 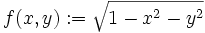 betrachtet. Der Definitionsbereich ist die Kreisscheibe B1(0,0) mit Radius 1 in der x,y-Ebene mit dem Mittelpunkt (0,0).
betrachtet. Der Definitionsbereich ist die Kreisscheibe B1(0,0) mit Radius 1 in der x,y-Ebene mit dem Mittelpunkt (0,0).Die Funktion f projiziert diesen Kreis auf die Oberfläche einer Halbkugel vom Radius 1 (die "obere Halbkugel"). Der Pol dieser Halbkugel ist ein Extremwert von f (ein Maximum). Für einen festen Wert von x ist dann f eine Funktion in y. Bei festem x ergeben die Punkte
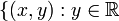 so dass
so dass 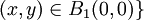 eine Strecke parallel zur y-Achse. Diese Strecke wird von f auf eine gekrümmte Linie auf der Oberfläche der Halbkugel projiziert.
eine Strecke parallel zur y-Achse. Diese Strecke wird von f auf eine gekrümmte Linie auf der Oberfläche der Halbkugel projiziert.Die partielle Ableitung von f nach y bestimmt unter diesen Voraussetzungen die Steigung der Tangente an diese Kurve im Punkt f(x,y). Für jeden Parameter einer Funktion f kann man partielle Ableitungen bestimmen.
Literatur
- Kurt Endl; Wolfgang Luh: Analysis II, Akademische Verlagsgesellschaft Frankfurt am Main, 1974
Wikimedia Foundation.