Flussnetzwerk

Ein Netzwerk N=(V, E, s, t, c) ist in der Graphentheorie ein gerichteter Graph ohne Mehrfachkanten mit zwei ausgezeichneten Knoten, einer Quelle s und einer Senke t aus V sowie einer Kapazitätsfunktion c, die jeder Kante (x,y) aus E eine nicht-negative, reellwertige Kapazität c(x,y) zuweist.

Ein s-t-Fluss ist eine Funktion f, die jeder Kante (x,y) im Netzwerk einen nicht-negativen reellen Flusswert f(x,y) zuweist. Dabei müssen folgende Bedingungen erfüllt sein:

1. Kapazitätsbeschränkung:

   Der Fluss einer Kante ist höchstens so groß wie die Kapazität auf der Kante, d.h. es gilt

   $\forall (x,y)\in E:f(x,y)\leq c(x,y)$.

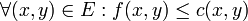2. Flusserhaltung:

   Abgesehen von der Quelle s und der Senke t muss in jeden Knoten genau so viel hineinfließen wie herausfließen, d.h.

   $\forall x\in V \setminus \{ s,t \} :\sum_{y \in x^+}f(x,y)=\sum_{y\in x^-}f(y,x)$

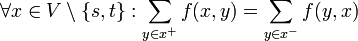
   Dabei sind x ⁺ und x ⁻ die Mengen der Knoten die mit x durch eine (von x aus gesehen) ausgehende bzw. eingehende Kante verbunden sind.

Der Wert val(f) eines s-t-Flusses f ist die Summe der Flusswerte der eingehenden Kanten abzüglich der Flusswerte der ausgehenden Kanten der Senke t, 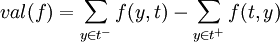$val(f) = \sum_{y\in t^-}f(y,t) - \sum_{y\in t^+}f(t,y)$. Dass der Wert der Flusses genauso gut an der Quelle s als Summe der ausgehenden abzüglich der eingehenden Flusswerte an s berechnet werden kann, folgt aus Flusserhaltungsbedingung. Es gilt $val(f) = \sum_{y\in s^+}f(s,y) - \sum_{y\in s^-}f(y,s)$.

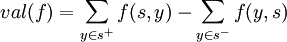Eine Teilmenge der Knoten in einem Netzwerk, die s aber nicht t enthält, nennt man einen Schnitt. Die Kapazität eines Schnittes ist die Summe der Kapazitäten der aus dem Schnitt herausführenden Kanten. Laut dem Max-Flow-Min-Cut-Theorem kann der Wert eines maximalen Flusses im Netzwerk nicht größer als die Kapazität eines beliebigen und somit auch eines minimalen Schnittes sein.

Das Restnetzwerk (auch: Residualgraph) bezüglich eines zulässigen Flusses ist ein Graph, der alle Kanten des ursprünglichen Netzwerkes enthält, mit um den jeweiligen Flusswert verminderten Kantenkapazitäten.

Beispiel

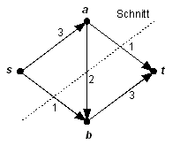
Nebenstehendes Beispiel zeigt ein einfaches Netzwerk und einen möglichen Schnitt darin. Die Kapazität des Schnittes ist c(s,b) + c(a,b) + c(a,t) = 1 + 2 + 1 = 4.

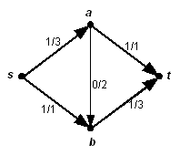
Im zweiten Bild ist ein möglicher Fluss angegeben. Die Belegung steht zusammen mit der Kapazität an den einzelnen Kanten. Der Wert des Flusses ist 2.

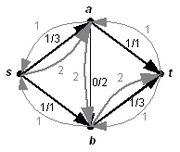
Aus dem gegebenen Fluss ergibt sich das in Grau dargestellte Restnetzwerk. Auf dem Pfad s, a, b, t lässt sich der Fluss um den Wert 2 erhöhen.

Algorithmen

Der Algorithmus von Ford und Fulkerson findet in einem Netzwerk einen maximalen Fluss.

Mit dem Algorithmus von Dinic, der alle kürzesten s-t-Pfade in einem Schritt findet, ist eine Laufzeit von O(|V|²|E|) möglich; wenn alle Kanten nur 0 oder 1 als Kapazitäten haben dürfen, verbessert sich die Laufzeit auf O(|V|^2/3|E|).

Die folgende Tabelle gibt eine Übersicht der entwickelten Fluss-Algorithmen und ihrer Laufzeiten:

Jahr	Autor	Laufzeit (n = Anzahl Knoten, m = Anzahl Kanten, U = Kante mit größter Kapazität im Graph)
1956	Ford-Fulkerson	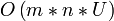$O\left(m*n*U\right)$
1969	Edmonds-Karp	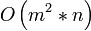$O\left(m^2 *n\right)$
1970	Dinic	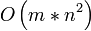$O\left(m*n^2\right)$
1973	Dinic-Gabow	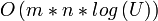$O\left(m*n*log\left(U\right)\right)$
1974	Karzanov	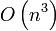$O\left(n^3\right)$
1977	Cherkassky	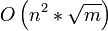$O\left(n^2 *\sqrt{m}\right)$
1980	Galil-Naamad	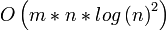$O\left(m*n*log\left(n\right)^2\right)$
1983	Sleator-Tarjan	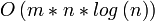$O\left(m*n*log\left(n\right)\right)$
1986	Goldberg-Tarjan	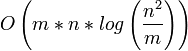$O\left(m*n*log\left(\frac{n^2}{m}\right)\right)$
1987	Ahuja-Orlin	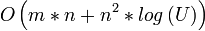$O\left(m*n+n^2*log\left(U\right)\right)$
1987	Ahuja-Orlin-Tarjan	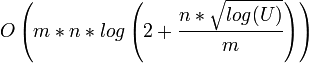$O\left(m*n*log\left(2+\frac{n*\sqrt{log(U)}}{m}\right)\right)$
1990	Cheriyan-Hagerup-Mehlhorn	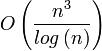$O\left(\frac{n^3}{log\left(n\right)}\right)$
1990	Alon	$O\left(m*n+\sqrt[3]{n^8}*log\left(n\right)\right)$
1992	King-Rao-Tarjan	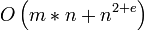$O\left(m*n+n^{2+e}\right)$
1993	Philipps-Westbrook	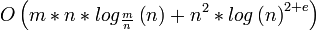$O\left(m*n*log_{\frac{m}{n}}\left(n\right)+n^2 *log\left(n\right)^{2+e}\right)$
1994	King-Rao-Tarjan	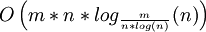$O\left(m * n*log_{\frac{m}{n*log(n)}}(n)\right)$
1997	Goldberg-Rao	$O\left(min(\sqrt{m}, \sqrt[3]{n^2}) *m* log\left(\frac{n^2}{m}\right)*log(U)\right)$

Anwendung

Flussalgorithmen lassen sich beispielsweise zur Berechnung der Knotenzusammenhangszahl und Kantenzusammenhangszahl verwenden.

Bipartiter Graph mit der Knotenmenge A (rot) und B (grün) und der ergänzten Quelle s und Senke t

Ferner kann durch Flussalgorithmen eine maximale Paarung in einem bipartiten Graphen gefunden werden. In einem solchen Graph kann die Menge der Knoten V in die disjunkten Teilmengen A und B eingeteilt werden. Erzeugt man nun ein Netzwerk N, indem man eine Quelle s hinzufügt und diese mit jedem Knoten aus A verbindet und entsprechend alle Knoten aus B mit einer Senke t und ordnet man all diesen Kanten die Kapazität 1 sowie allen anderen Kanten aus dem originalen Graphen G eine beliebige Kapazität 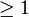$\geq1$ zu, dann entspricht ein maximaler Fluss in N einer maximalen Paarung in G und umgekehrt.

Siehe auch

• Schnitt (Graphentheorie)

Literatur

• L. R. Ford, D. R. Fulkerson: Flows in Networks. 1962, ISBN 0691079625, ISBN 978-0691079622.