Algorithmus von Ford und Fulkerson

Der Algorithmus von Ford und Fulkerson (nach seinen Erfindern Lester Randolph Ford junior und Delbert Ray Fulkerson^[1]) dient der Berechnung eines maximalen s-t-Flusses in einem Netzwerk. Er sucht sukzessiv nach flussvergrößernden Pfaden im Residualgraphen (Restnetz), vergrößert den Fluss entlang dieser Pfade und hält an, falls kein solcher Pfad mehr existiert. Wenn die Kapazitäten der Kanten irrationale Zahlen sind, kann es sein, dass der Algorithmus nicht konvergiert. Außerdem kann der Algorithmus, bei ungeschickter Verteilung der Kapazitäten, eine schlechte Laufzeit haben. Er dient als Grundlage für den besseren Edmonds-Karp-Algorithmus.

Der Algorithmus

Gegeben sei ein Netzwerk N = (G,u,s,t), bestehend aus einem endlichen, gerichteten Graphen G = (V(G),E(G)) mit einer Quelle $s\in V(G)$, einer Senke $t\in V(G)$ und einer Kapazitätsfunktion $u:E(G)\to\mathbb{R}_{\geq 0}$, die jeder Kante e eine nichtnegative reelle Zahl u(e) als Kapazität zuordnet.

Der Algorithmus verändert in jedem Durchlauf einen s-t-Fluss im Netzwerk N, also eine Abbildung $f:E(G)\to\mathbb{R}_{\geq 0}$ mit den Eigenschaften

• Kapazitätsbeschränkung: Für jede Kante e ist $0\le f(e)\le u(e)$.
• Flusserhaltung: Für jeden Knoten $x\in V(G)\setminus\{s,t\}$ gilt:

  $\sum_{e\in \delta^+(x)}f(e)=\sum_{e\in \delta^-(x)}f(e)$.

Hierbei bezeichnet δ ⁺ (x) die Menge der aus x hinausführenden Kanten und δ ⁻ (x) die Menge der in x hineinführenden Kanten.

Der Algorithmus sucht in jedem Schritt einen Weg von s nach t im Residualgraphen. Der Residualgraph G_f teilt sich mit G dieselbe Knotenmenge und enthält die Kanten von G, die von f nicht ausgelastet sind, ergänzt um sogenannte Rückkanten: Für jede Kante $e=(v, w)\in E(G)$ mit f(e) > 0 enthält E(G_f) jeweils zusätzlich eine Rückkante $\overleftarrow{e}=(w,v)$. Formal gilt also: $G_f = (V(G), \{e\in E(G) \mid f(e)<u(e)\}\dot{\cup} \{\overleftarrow{e} \mid \exists e\in E(G): e=(v,w) \ \and \ f(e)>0 \ \and \ \overleftarrow{e}=(w,v)\})$ Dazu werden Residualkapazitäten u_f definiert, die jeder Kante $e\in E(G)$ zuordnen, um wie viel der Fluss f auf e noch erhöht werden kann, und jeder Rückkante $\overleftarrow{e}\in E(G_f)\setminus E(G)$ zuordnen, um wie viel der Fluss auf der zugehörigen Hinkante $e\in E(G)$ verringert werden kann. Also formal:

$u_f(e) = \begin{cases} u(e) - f(e) & \text{wenn } e\in E(G) \\ f(g) & \text{wenn } e=\overleftarrow{g} \text{ die R}\mathrm{\ddot u}\text{ckkante der Kante } g \text{ ist.} \end{cases}$

Zur Initialisierung kann man den Nullfluss, der jeder Kante e den Wert 0 zuordnet, verwenden. Der Algorithmus beschreibt sich wie folgt:

1. (Initialisierung:) Setze f(e): = 0 für jede Kante $e\in E(G)$.
2. Solange es im Residualgraphen G_f einen Weg von s nach t gibt, bestimme einen solchen Weg W und tue:

   Bestimme $\gamma:=\min\{u_f(e) \mid e\in E(W)\}$.

   Für alle $e\in E(W)\cap E(G)$ setze: f(e): = f(e) + γ.

   Für alle $\overleftarrow{e}\in E(W)\setminus E(G)$ setze für die zugehörige Hinkante e: f(e): = f(e) − γ.

Sind alle Kapazitäten rational, berechnet der Algorithmus nach endlich vielen Schritten einen maximalen s-t-Fluss.

Beispiel

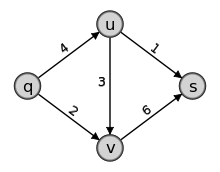
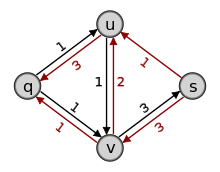
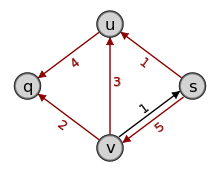
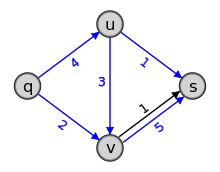
Gegeben sei ein Netzwerk mit vier Knoten q,u,v,s und den Kapazitäten 1, 2, 3, 4, 6 wie in der Grafik. Gesucht ist ein maximaler q-s-Fluss. Initialisiere den Fluss mit f0((q,u)) = f0((q,v)) = f0((u,v)) = f0((u,s)) = f0((v,s)) = 0.
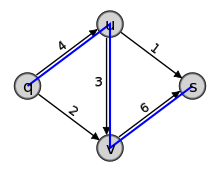
1. (a) Wähle irgendeinen Pfad von q nach s. Dieser Pfad (in der Grafik blau) hat die Kapazität 3, da dies die minimale Kantenkapazität der Kanten auf dem Pfad ist. Vergrößere den Fluss entlang des Pfades um 3, dies ergibt f1((q,u)) = f1((u,v)) = f1((v,s)) = 3, es bleibt f1((q,v)) = f1((u,s)) = 0.
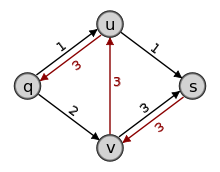
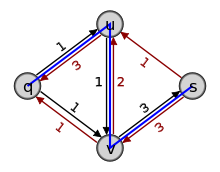
1. (b) Bilde das Residualnetzwerk $N_{f_0}$. Hier verringern sich die Kapazitäten der Kanten (q,u) und (v,s), die Kante (u,v) fällt weg, dafür kommen drei Rückkanten (u,q), (v,u) und (s,v) hinzu, die rot dargestellt sind. Auf diesen ergeben sich die Residualkapazitäten $u_{f_1}((u,q))=u_{f_1}((v,u))=u_{f_1}((s,v))=3$.
2. (a) Wähle irgendeinen Pfad von q nach s im Residualnetzwerk. Der in der Grafik blau gezeichnete Weg hat die minimale Kapazität 1. Vergrößere den Fluss entlang des Pfades um eins, dies ergibt f2((q,u)) = f2((v,s)) = 3, f2((u,v)) = 2 und f2((q,v)) = f2((u,s)) = 1.
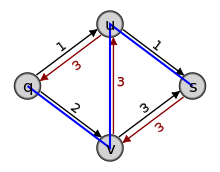
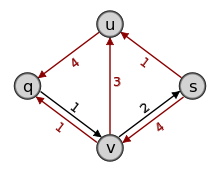
2. (b) Bilde das Residualnetzwerk $N_{f_2}$, worin der Fluss f2 zu sehen ist. Die Kapazität der Kante (q,v) verringert sich um eins und eine neue Rückkante (v,q) wird gebildet. Die Kapazität der Kante (u,v) erhöht sich um eins, so dass die Hinkante (u,v) wieder entsteht. Die Kapazität der Kante (u,s) wird um eins verringert, wodurch die Hinkante (u,s) entfernt wird. Es ergeben sich die Residualkapazitäten $u_f((v,q))=u_f((s,u))=1,\ u_f((v,u))=2,\ u_f((u,q))=u_f((s,v))=3$
3. (a) Wähle irgendeinen Pfad von q nach s im Residualnetzwerk. Der hier Gewählte (blau markiert) hat die Kapazität 1, also ist f3((q,u)) = f3((v,s)) = 4, f3((u,v)) = 3, und f3((q,v)) = f3((u,s)) = 1.
3. (b) Bilde das Residualnetzwerk $N_{f_3}$; darin findet man den Fluss f3 durch Umkehrung der roten Kanten.
4. (a) Wähle irgendeinen Pfad im Residualnetzwerk $N_{f_3}$ von q nach s: In dieser Situation gibt es nur noch einen Pfad, nämlich (q,v,s). Dieser hat die minimale Kapazität eins. Es ergibt sich $f_4((q,u))=4,\quad f_4((q,v))=2,\quad f_4((u,v))=3,\quad f_4((u,s))=1,\quad f_4((v,s))=5$.
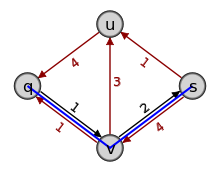
4. (b) Bilde das Residualnetzwerk $N_{f_4}$. In q kommen nur noch Kanten an, es gibt also keinen Weg mehr von q nach s. Damit ist f4 ein maximaler Fluss durch das eingangs gegebene Netzwerk.

Ein maximaler Fluss im Beispielnetzwerk

Der Algorithmus stoppt hier, da im verbliebenen Residualnetzwerk kein Pfad von q nach s mehr existiert. Den erreichten Fluss f₄ sieht man, indem man zu jeder roten Kante ihre Zahl als Größe des Flusses auf der umgedrehten Kante nimmt. Die verbleibenden schwarzen Kanten geben die unbenutzten Residualkapazitäten an.

Zur Korrektheit des Algorithmus

Ford und Fulkerson konnten beweisen, dass ein s-t-Fluss f in einem Netzwerk N genau dann maximal ist, wenn es keinen augmentierenden Pfad gibt, d.h., wenn das Restnetzwerk N_f keinen Pfad von s nach t besitzt. Daher gilt:

Falls der Algorithmus von Ford und Fulkerson zum Stehen kommt, ist ein maximaler s-t-Fluss gefunden.

Dabei muss der maximale s-t-Fluss nicht eindeutig bestimmt sein.

Bei der Durchführung des Algorithmus vergrößert sich der betrachtete Fluss mit jedem Schritt. Daraus folgt eine wichtige Tatsache für ganzzahlige Netzwerke:

Sind alle Kapazitäten des gegebenen Netzwerks nichtnegative ganze Zahlen, so kommt der Algorithmus von Ford und Fulkerson nach endlich vielen Schritten zum Stehen und liefert einen maximalen s-t-Fluss, der außerdem ganzzahlig ist.

Sind alle Kapazitäten rationale Zahlen, so erhält man durch Multiplikation mit dem Hauptnenner ein ganzzahliges Netzwerk, und kann so die folgende Aussage beweisen:

Sind alle Kapazitäten des gegebenen Netzwerks nichtnegative rationale Zahlen, so kommt der Algorithmus von Ford und Fulkerson nach endlich vielen Schritten zum Stehen und liefert einen maximalen s-t-Fluss, der außerdem nur rationale Werte hat.

Falls irrationale Zahlen als Kapazitäten vorkommen, gilt das nicht mehr: Ford und Fulkerson konstruierten ein Beispiel eines Netzwerkes mit 10 Knoten und 48 Kanten, bei dem ihr Algorithmus bei geeigneter Auswahl der augmentierenden Pfade nicht zum Stehen kommt und auch nicht gegen einen maximalen Fluss konvergiert^[2]. Im Jahr 1995 fand Uri Zwick ein Beispiel mit 6 Knoten und 8 Kanten und einem derartigen Verhalten^[3].

Zeitkomplexität

Einerseits benötigt jeder Schleifendurchlauf des Algorithmus lediglich $\mathcal{O}(|V(G)|+|E(G)|)$ Zeit (siehe Landau-Notation), aber andererseits hängt die benötigte Anzahl der Schleifendurchläufe von der Größe der Kapazitäten ab. Es ist möglich, die flussvergrößernden Pfade sehr ungünstig zu wählen.

Wählt man in jedem Schritt immer einen kürzesten augmentierenden Pfad zur Vergrößerung des Flusses, so erhält man den Algorithmus von Edmonds und Karp, der stets in Laufzeit $\mathcal{O}(|V(G)| \cdot |E(G)|^2)$ einen maximalen s-t-Fluss konstruiert. Eine weitere Verbesserung mit Hilfe zusätzlicher Techniken bringt der Algorithmus von Dinic mit einer (worst-case)-Komplexität von $\mathcal{O}(|V(G)|^2 \cdot |E(G)|)$.

Weblinks

• Ein anschauliches Programm zu Ford-Fulkerson und weiteren Algorithmen (Java-Applet, englisch)
• Ein kommentierter Quellcode in C (englisch)

 Commons: Ford-Fulkerson's algorithm – Sammlung von Bildern, Videos und Audiodateien

Quellen

• Bernhard Korte, Jens Vygen: Kombinatorische Optimierung: Theorie und Algorithmen. Aus dem Englischen von Rabe von Randow. Springer-Verlag, Berlin Heidelberg 2008, ISBN 978-3-540-76918-7

Einzelnachweise

1. ↑ Lester Randolph Ford junior, Delbert Ray Fulkerson: Maximal flow through a network, Canad. J. Math. 8 (1956), 399-404.
2. ↑ Lester Randolph Ford junior, Delbert Ray Fulkerson: Flows in Networks, Princeton University Press 1962
3. ↑ Uri Zwick: The smallest networks on which the Ford-Fulkerson maximum flow procedure may fail to terminate, Theoretical Computer Science 148, 165-170 (1995).