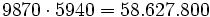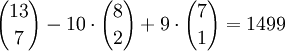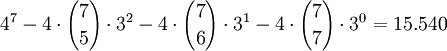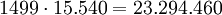Four of a kind

Im Kartenspiel Poker beschreibt der Begriff Hand die besten fünf Karten, die ein Spieler nutzen kann. Die Rangfolge der einzelnen Kartenkombinationen ist bei allen Spielvarianten gleich, lediglich ihre Wahrscheinlichkeit variiert. So ist bei der Spielvariante Texas Hold'em sogar das Paar wahrscheinlicher als High Card, rangiert aber dennoch höher. Die wichtigste Änderung stellt ein Deck mit einem Joker dar. Die bestmögliche erreichbare Hand ist bei einem solchen Deck ein Fünfling, während die beste Hand bei einem normalen französischen Blatt der Royal Flush ist.

Allgemeine Regeln

• Falls eine Gleichheit bei der Kombination herrscht, entscheidet für gewöhnlich die Höhe der einzelnen Karten. Dabei gilt folgende, absteigende Reihenfolge: Ass – König – Dame – Bube – 10 – 9 – 8 – 7 – 6 – 5 – 4 – 3 – 2. Ist solch eine Karte entscheidend, so hat der betroffene Spieler den besseren Kicker.
• Eine Hand besteht immer aus fünf Karten. Deshalb ist es auch nicht möglich, dass der Kicker bei zwei gleich hohen Straights entscheidet, da diese ja bereits aus fünf Karten bestehen.
• Karten werden zuerst nach der Höhe ihrer Kombination gewertet und erst danach nach der Höhe innerhalb der Kombination: Zwei Paare aus Zweien und Dreien sind also besser als Ein Paar Asse.
• Es gibt keine Hierarchie der Farben mit Einfluss auf die Hand, die Stärke eines Flush ist nicht davon abhängig, zu welcher der vier Farben die fünf gleichfarbigen Karten gehören.

Anzahl möglicher Kombinationen

Insgesamt sind

${52 \choose 5} = {{52!} \over {5! (52-5)!}} = \frac{52 \cdot 51 \cdot 50 \cdot 49 \cdot 48}{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} = 2.598.960$

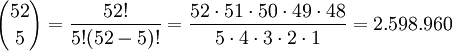
verschiedene Hände möglich.

Kombinationsmöglichkeiten bei 5 aus 52 Karten

Hand	Möglichkeiten	Wahrscheinlichkeit	kumuliert	Verhältnis
Straight Flush	36+4	0,00154%	0,00154%	64.973 : 1
Vierling	624	0,0240%	0,0256%	4.164 : 1
Full House	3.744	0,144%	0,170%	693 : 1
Flush	5.108	0,197%	0,367%	508 : 1
Straight	10.200	0,392%	0,76%	254 : 1
Drilling	54.912	2,11%	2,87%	46,3 : 1
Zwei Paare	123.552	4,75%	7,62%	20,0 : 1
Paar	1.098.240	42,3%	49,9%	1,37 : 1
Höchste Karte	1.302.540	50,1%	100%	1 : 1
Total	2.598.960	100%	100%	1 : 1

Royal Flush

Diese Hand ist eigentlich ein Straight Flush, wird durch ihre Rolle als beste Hand im Poker und ihre Seltenheit jedoch gesondert betrachtet. Ein Royal Flush, wie z. B. A♣ K♣ Q♣ J♣ 10♣, ist ein Straight Flush mit dem Ass als höchste Karte, somit also der höchste Straight Flush.

Diese Hand ist so selten, dass sie bisher erst dreimal bei einer Poker-Übertragung im deutschen Fernsehen zu sehen war. In dem sehr unwahrscheinlichen Fall, dass z. B. beim Draw Poker, zwei Spieler einen Royal Flush halten, wird der Pot geteilt. Bei den Hold'em-Varianten, bei denen mit Gemeinschaftskarten gespielt wird, ist eine solche Situation nur möglich, wenn der Royal Flush komplett offen auf dem Tisch liegt, also die 5 Gemeinschaftskarten (board) den Royal Flush zeigen, bei der Variante Omaha Hold'em, in der es auch Gemeinschaftskarten gibt, ist eine solche Situation nicht möglich.

Beispiele:

• A♣ K♣ Q♣ J♣ 10♣ schlägt K♣ Q♣ J♣ 10♣ 9♣

Ein Splitpot ist nur möglich, wenn das Board A♣ K♣ Q♣ J♣ 10♣ ( oder andere Farbe ) ist. In diesem Fall spielen alle Spieler den Royal Flush vom Board.

Anzahl möglicher Kombinationen

Es gibt eine mögliche höchste Karte (Ass) und vier verschiedene Farben:

${1\choose 1}{4 \choose 1} = 4$

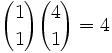
Straight Flush

Die verschiedenen Straight Flushs (für: Einfarbige Straßen; darunter auch der Royal Flush, s. o.) sind die bestmöglichen Kartenkombinationen. Ein Beispiel ist eine Hand wie Q♠ J♠ 10♠ 9♠ 8♠, die fünf Karten hintereinander in derselben Farbe enthält. Zwei konkurrierende Straight Flushs werden nach ihrer höchsten Karte bewertet, vergleichbar mit einem straight. Die Wahrscheinlichkeit des Auftretens eines Straight Flushs ist noch geringer als diejenige von vier Karten gleichen Rangs (z. B. vier Buben), deshalb ist der Straight Flush die zweithöchst gewertete aller Pokerhände. Hier sind auch Straights mit 5 als höchster Karte möglich, wie etwa 5♦ 4♦ 3♦ 2♦ A♦. Diese Hand ist auch als steel wheel bekannt.

Beispiele:

• 7♥ 6♥ 5♥ 4♥ 3♥ schlägt 5♠ 4♠ 3♠ 2♠ A♠
• J♣ 10♣ 9♣ 8♣ 7♣ „splittet“ J♦ 10♦ 9♦ 8♦ 7♦ (split pot)

Anzahl möglicher Kombinationen (ohne Royal Flush)

Es gibt (ohne Ass) neun verschiedene mögliche höchste Karten und vier verschiedene Farben:

${9\choose 1}{4 \choose 1} = 36$

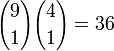
Vierling

Ein Vierling, oder Poker, im Englischen auch four of a kind oder quads genannt, ist eine weitere Pokerhand. Ein Beispiel dafür ist 9♣ 9♠ 9♦ 9♥ J♥. Ein Vierling enthält vier Karten desselben Wertes. Der Vierling steht über dem Full House und unter einem Straight Flush. Es entscheidet die Höhe des Vierlings. Liegt bereits ein Vierling unter den Gemeinschaftskarten, sodass alle verbliebenen Spieler diesen Vierling nutzen können, entscheidet die Höhe des Kickers, bei Gleichheit kommt es zu einem split pot.

Beispiele:

• 10♣ 10♦ 10♥ 10♠ 5♦ schlägt 6♦ 6♥ 6♠ 6♣ K♠
• 10♣ 10♦ 10♥ 10♠ Q♣ schlägt 10♣ 10♦ 10♥ 10♠ 5♦ aufgrund des besseren Kickers
• 10♣ 10♦ 10♥ 10♠ Q♣ „splittet“ 10♣ 10♦ 10♥ 10♠ Q♦ (split pot)

Anzahl möglicher Kombinationen

Jeder der dreizehn Werte kann sich zu einem Vierling entwickeln. Bleiben (52-4) = 48 restliche Karten, die als Kicker dienen:

${13 \choose 1}{48 \choose 1} = 624$

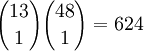
Full House

Ein Full House, zu deutsch volles Haus, manchmal auch volles Boot genannt, entspricht einer Hand wie 3♣ 3♠ 3♦ 6♣ 6♥. Ein Full House besteht also aus einem Drilling und einem Paar. Damit liegt die Hand in der Wertigkeit unter einem Vierling und über einem Flush. Die Höhe des Drillings entscheidet. Können zwei Spieler mit den Gemeinschaftskarten ein Full House mit dem gleichen Drilling zusammenstellen, entscheidet die Höhe des Paars, bei Gleichheit kommt es zu einem split pot.

Beispiele:

• 10♠ 10♥ 10♦ 4♠ 4♦ schlägt 9♥ 9♣ 9♠ A♥ A♣ aufgrund des besseren Drillings
• Q♥ Q♦ Q♣ 8♥ 8♣ 8♥ 8♣
• 10♠ 9♠ 4♠ 8♥ 8♣ schlägt 9♥ 9♣ 9♠ A♥ A♣ aufgrund des besseren Drillings
• Q♣ 8♥ 8♣ „splittet“ Q♥ Q♦ Q♠ 8♥ 8♣ (split pot)

Anzahl möglicher Kombinationen

Der Drilling kann von dreizehn Werten und drei verschiedenen Farben sein. Das Paar kann eines von den verbliebenen zwölf Werten sein und besteht aus zwei von vier Farben:

${13 \choose 1}{4 \choose 3}{12 \choose 1}{4 \choose 2} = 3.744$

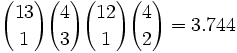
Flush

Ein Flush ist eine Hand wie etwa Q♣ 10♣ 7♣ 6♣ 4♣, die aus fünf Karten derselben Farbe besteht. Zwei Flushs werden nach ihrer höchsten Karte bewertet. Ist diese gleich, entscheidet die zweithöchste, dann die dritthöchste Karte und so weiter. Ein Flush muss nicht aus aufeinanderfolgenden Karten gebildet werden. Ist das aber der Fall, so spricht man von einem Straight Flush. Die Farbe des Flushs spielt in der Reihenfolge keine Rolle.

Beispiele:

• A♥ Q♥ 10♥ 5♥ 3♥ schlägt K♠ Q♠ J♠ 9♠ 6♠ (ace high flush gewinnt)
• A♦ K♦ 7♦ 6♦ 2♦ schlägt A♥ Q♥ 10♥ 5♥ 3♥ (flush, ace king high gewinnt)
• Q♥ 10♥ 9♥ 5♥ 2♥ „splittet“ Q♠ 10♠ 9♠ 5♠ 2♠ (split pot)

Anzahl möglicher Kombinationen

Der Flush besteht aus fünf Karten derselben Farbe. Von jeder Farbe gibt es dreizehn Karten. Es gibt vier verschiedene Farben. Von der Zahl ziehen wir die 36 möglichen straight flushs und die vier möglichen royal flushs ab, die jeweils extra gewertet werden:

${13 \choose 5}{4 \choose 1} - 36 - 4 = 5.108$

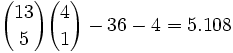
Straight

Hauptartikel: Straße (Kartenspiel)

Ein Straight, im Deutschen auch Straße, ist eine Hand wie beispielsweise Q♣ J♠ 10♠ 9♥ 8♥, die aus fünf aufeinanderfolgenden Karten verschiedener Farben gebildet wird. Sind die Farben der fünf Karten jedoch identisch, spricht man von einem Straight Flush. Die Hand ist stärker als ein Drilling und schwächer als ein Flush. Sind zwei Straights im Umlauf, wird nach der höchsten Karte gewertet. Ist diese gleich, gibt es einen split pot. Straights mit fünf als höchste Zahl, also A - 2 - 3 - 4 - 5, sind erlaubt, Straights wie K - A - 2 - 3 - 4 (round the corner straight) jedoch nicht, wenn nicht ausdrücklich vereinbart. Andere Varianten, wie skip straight (3 - 5 - 7 - 9 - J) sollten auch vor Beginn der Spielrunde vereinbart werden, ggf. inklusive ihrer Bewertung.

Beispiele:

• 8♠ 7♠ 6♥ 5♥ 4♠ schlägt 6♦ 5♠ 4♦ 3♥ 2♣ (eight high straight)
• 8♠ 7♠ 6♥ 5♥ 4♠ „splittet“ 8♥ 7♦ 6♣ 5♣ 4♥ (split pot)

Anzahl möglicher Kombinationen

Ein Straight besteht aus fünf Karten. Er besteht aus einer der zehn möglichen höchsten Karten. Jede Karte kann eine beliebige der vier Farben haben. Wie bei den flushs werden die 36 straight flushs und die vier royal flushs abgezogen:

${10 \choose 1}{4 \choose 1}^5 - 36 - 4 = 10.200$

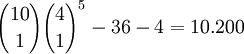
Drilling

Drilling, im Englischen auch three of a kind genannt, ist eine Hand wie 2♦ 2♠ 2♥ K♠ 6♠, die drei Karten desselben Wertes und zwei andere Karten enthält. Es ist über den zwei Paaren und unter dem Straight angeordnet. Können zwei Spieler aus den Gemeinschaftskarten einen gleich hohen Drilling bilden, entscheidet die Höhe des ersten Kickers, bei Gleichheit der zweite Kicker.

Beispiele:

• 8♠ 8♥ 8♦ 5♠ 3♣ schlägt 5♣ 5♥ 5♦ Q♦ 10♣ (three eights gewinnt)
• 8♠ 8♥ 8♦ A♣ 2♦ schlägt 8♣ 8♥ 8♦ 5♠ 3♣

Wenn auch wertungstechnisch identisch, ergeben sich bei Spielen mit Gemeinschaftskarten zwei grundverschiedene Spielsituationen.

• Ein Set ist ein Drilling, das aus einem Pocket Pair entstanden ist, was eine sehr starke Hand darstellt, zumal sie schwer lesbar für den Gegner ist.
• Trips ist ein Drilling mit einer Karte der Starthand und einem offenen Paar. Diese Kombination kann nie die nuts sein.

Anzahl möglicher Kombinationen

Jeder der dreizehn Werte kann einen Drilling bilden. Enthalten sind drei der vier Farben eines Wertes. Die anderen beiden Karten können zwei der zwölf verbliebenen Werte in vier verschiedenen Farben haben:

${13 \choose 1}{4 \choose 3}{12 \choose 2}{4 \choose 1}^2 = 54.912$

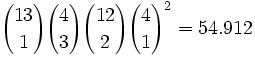
Zwei Paare

Eine Hand wie J♥ J♣ 4♣ 4♠ 9♠, nennt man Zwei Paare, engl. two pair. Oftmals werden die Paare auch genannt, wie etwa Zwei Paare, Asse und Achten. Sie besteht aus zwei Paaren und einer anderen Karte. Bei mehreren doppelten Paaren entscheidet das höhere Paar, dann das zweithöchste und gegebenenfalls der Kicker. Die Hand ist unter dem Drilling und über dem Paar angeordnet.

Beispiele:

• K♥ K♦ 2♣ 2♦ J♥ schlägt J♦ J♠ 10♠ 10♣ 9♠ (kings up gewinnt)
• 4♠ 4♣ 3♠ 3♥ K♦ (fours and threes, king kicker) schlägt 4♥ 4♦ 3♦ 3♣ 10♠

Anzahl möglicher Kombinationen

Jedes der zwei Paare kann einen der dreizehn Werte und zwei der vier Farben haben. Der Kicker kann einen der elf verbliebenen Werte und eine beliebige Farbe haben:

${13 \choose 2}{4 \choose 2}^2{11 \choose 1}{4 \choose 1} = 123.552$

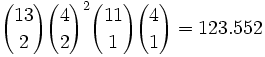
Paar

Ein Paar, engl. one pair, ist eine Hand, bei der ein Wert doppelt vorhanden ist, wie etwa 4♥ 4♠ K♠ 10♦ 5♠, die zusätzlich drei andere Karten enthält. Die Hand ist schwächer als Zwei Paare und besser als die so genannte High Card. Können zwei Spieler gleich hohe Paare vorweisen, entscheidet die Höhe des ersten Kickers, bei Gleichheit der zweite und ggf. der dritte Kicker.

Beispiele:

• 10♣ 10♠ 6♠ 4♥ 2♥ schlägt 9♥ 9♣ A♥ Q♦ 10♦
• 10♥ 10♦ J♦ 3♥ 2♣ schlägt 10♣ 10♠ 6♠ 4♥ 2♥
• 10♥ 10♦ J♦ 4♥ 3♣ schlägt 10♣ 10♠ J♠ 4♦ 2♥

Anzahl möglicher Kombinationen

Ein Paar kann dreizehn Werte und zwei von vier verschiedenen Farben haben. Die restlichen drei Karten können zwölf verschiedene Werte und vier Farben haben:

${13 \choose 1}{4 \choose 2}{12 \choose 3}{4 \choose 1}^3 = 1.098.240$

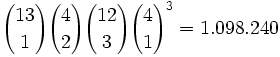
High Card

Eine High Card, auch no pair genannt, bedeutet keine der obigen Kombinationen. Ein Beispiel ist K♥ J♣ 8♣ 7♦ 3♠. Bei zwei konkurrierenden High Cards zählt der Kicker, bei Gleichheit der zweite Kicker und so weiter.

Beispiele:

• A♦ 10♦ 9♠ 5♣ 4♣ schlägt K♣ Q♦ J♣ 8♥ 7♥
• A♦ 10♦ 9♠ 5♣ 4♣ schlägt A♣ 9♦ 8♥ 5♠ 4♠

Anzahl möglicher Kombinationen

Die Anzahl ergibt sich aus der Differenz der Anzahl aller möglichen Hände und der Summe der von Royal Flush bis Paar oben aufgeführten Hände:

${52 \choose 5} - 1.296.420 = 1.302.540$

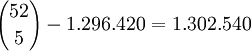
Ein anderer Ansatz ist, Werte und Farben unabhängig voneinander zu betrachten:

• Es müssen fünf verschiedene Werte vorkommen, dabei dürfen sie keine der – betrachtet man nur die Werte und lässt die Farben außen vor – zehn Straßen bilden.
• Die Farben dürfen keinen der vier Flushs bilden, wobei hier analog nur die Farben betrachtet werden und die Werte außen vor sind.

Diese beiden Zahlen werden miteinander multipliziert:

$\left[{13 \choose 5} - 10\right](4^5 - 4) = 1.302.540$

Kombinationsmöglichkeiten bei 7 aus 52 Karten (Texas Hold'em)

Hand	Möglichkeiten	Wahrscheinlichkeit	kumuliert	Verhältnis
Straight Flush	41.584	0,0311%	0,0311%	3216 : 1
Vierling	224.848	0,168%	0,199%	594 : 1
Full House	3.473.184	2,60%	2,80%	37,5 : 1
Flush	4.047.644	3,03%	5,82%	32,1 : 1
Straight	6.180.020	4,62%	10,4%	20,6 : 1
Drilling	6.461.620	4,83%	15,3%	19,7 : 1
Zwei Paare	31.433.400	23,5%	38,8%	3,26 : 1
Paar	58.627.800	43,8%	82,6%	1,28 : 1
Höchste Karte	23.294.460	17,4%	100%	4,74 : 1
Total	133.784.560	100%	100%	0 : 1

Beziehung zu Wahrscheinlichkeiten

Teilt man die Anzahl der Kombinationen für eine Hand durch die Gesamtzahl 2.598.960 der Kombinationen, so ergibt dies die Wahrscheinlichkeit, diese Hand zu erhalten, wenn man fünf Karten aus einem Pokerblatt zieht. Daher ist verständlich, dass jede Hand umso wertvoller ist, je weniger Kombinationen sie entspricht.

Jedoch gilt diese Wahrscheinlichkeitsaussage streng eben nur, wenn es keine Gemeinschaftskarten gibt und auch keine Karten getauscht werden können. Sowohl die Möglichkeit zum Kartentausch als auch die Möglichkeit der Auswahl aus Gemeinschaftskarten beeinflussen die Wahrscheinlichkeiten üblicherweise eher zugunsten wertvollerer Hände, während wohlgemerkt die Rangfolge der einzelnen Hände sich unverändert nach der oben angegebenen Reihenfolge ergibt.

Im Fall des Kartentausches kommt es naturgemäß auf die vom Spieler gewählte Strategie an, wie die Wahrscheinlichkeiten im Detail beeinflusst werden. Eine unabhängig von der Spielerstrategie gültige Berechnung ist somit nicht möglich, und auf die Bestimmung einer möglicherweise optimalen Tauschstrategie kann hier nicht eingegangen werden.

Auch im Falle von Gemeinschaftskarten verändern sich die Wahrscheinlichkeiten und sind um einiges komplizierter zu berechnen als in den obigen Überlegungen. Für den Fall Texas Hold'em sollen hier nur exemplarisch die Hände ein Paar und High Card verglichen werden.

Ein Paar bei Texas Hold'em

Damit aus sieben Karten ein Paar (aber nichts besseres) gebildet werden kann, müssen sechs verschiedene Werte auftreten, hiervon einer doppelt, jedoch keine Straße. Verboten sind hierbei zehn Straßen in Kombination mit einem weiteren Wert mit 13-5 Möglichkeiten; hierbei werden jedoch neun „Sechser-Straßen“ doppelt abgezogen.

Dies ergibt für die Werte

$\left[{13 \choose 6} - 10\cdot(13-5) + 9\right]\cdot {6 \choose 1} = 9870$

verschiedene Kombinationen.

Hinsichtlich der Farben muss man für die das Paar bildenden Karten zwei aus vier Farben wählen, während bei den übrigen Karten alles erlaubt ist außer vier gleichen Farben mit einer der beiden auch im Paar auftretenden Farben oder ansonsten fünf gleichen Farben.

Dies ergibt

${4 \choose 2}\cdot\left[4^5 - 2\cdot{5\choose 1}\cdot 3 - 4\right] = 5940$

verschiedene Farbkombinationen.

Die Gesamtkombinationen ergeben sich als Produkt, also

$9870\cdot 5940 = 58.627.800$

Kombinationen.

Teilt man durch die 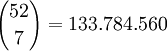${52\choose 7}=133.784.560$ Möglichkeiten insgesamt, so ergibt sich also eine Wahrscheinlichkeit von ca. 43,8%, bei Texas Hold'em ein Paar als beste Hand bilden zu können.

High Card bei Texas Hold'em

Damit aus sieben Karten gar keine wertvolle Kombination gebildet werden kann, müssen sieben verschiedene Werte auftreten, darunter jedoch keine Straße. Nach dem Prinzip von Inklusion und Exklusion muss man die Kombinationen aus zehn Straßen mit zwei anderen Werten abziehen, dann die doppelt abgezogenen Kombinationen aus neun Sechser-Straßen mit einem anderen Wert wieder addieren. Die acht Siebener-Straßen werden dreimal bei den Fünfer-Straßen abgezogen und zweimal bei den Sechser-Straßen addiert, sind also hierdurch bereits korrekterweise abgezogen.

Dies ergibt

${13\choose 7} - 10\cdot{8\choose 2} + 9\cdot{7\choose 1} = 1499$

Wertkombinationen.

Dem stehen

$4^7 - 4\cdot{7 \choose 5}\cdot 3^2 - 4\cdot{7\choose 6}\cdot 3^1 - 4\cdot{7\choose 7}\cdot 3^0 = 15.540$

Farbkombinationen gegenüber.

Wiederum als Produkt ergeben sich

$1499\cdot 15.540 = 23.294.460$

Kombinationen insgesamt und somit eine Wahrscheinlichkeit von nur ca. 17,4%, bei Texas Hold'em lediglich High Card zu erzielen.

Weblinks