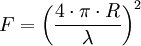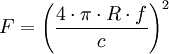Freifelddämpfung

Die Freiraumdämpfung beschreibt die Reduzierung der Leistungsdichte bei der Ausbreitung elektromagnetischer Wellen im freien Raum, also ohne Störeinflüsse von zusätzlich dämpfenden Medien (wie zum Beispiel der Luft) oder Störungen durch Reflexionen. Idealerweise wird eine Freiraumdämpfung im Vakuum, beispielsweise im Weltraum bei Richtfunkverbindungen von oder zu Satelliten auftreten und ist ein wichtiges Kriterium zur Berechnung notwendiger Sendeleistungen und Empfängerempfindlichkeiten. Zusätzlich berücksichtigt die Freiraumdämpfung die Abhängigkeit der Empfangsapertur von der Wellenlänge.

Entstehung der Freiraumdämpfung

Leistungsdichte auf einer Kugeloberfläche

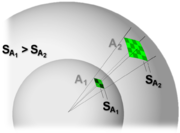
Wird von einem isotropen Kugelstrahler hochfrequente Leistung P abgestrahlt, so verteilt sich diese gleichmäßig in alle Richtungen. Demzufolge bilden Flächen gleicher Leistungsdichte S Kugeln um den Strahler. Bei größer werdendem Kugelradius R verteilt sich die Energie auf eine größere Fläche A = 4 π · R² um den Strahler herum. Oder anders ausgedrückt: Bezogen auf eine angenommene Fläche wird die Leistungsdichte S an der Fläche mit steigendem Abstand geringer:

(1) S = P /(4 π R²)

Der Ausschnitt der Kugeloberfläche kann bei den relativ kleinen Abmessungen gegenüber einer sehr großen Entfernung als eine ebene Wellenfront betrachtet werden. Eine Empfangsantenne entnimmt aus dieser Wellenfront Energie, die von der Wirkfläche A_W der Antenne abhängt. Die Wirkfläche einer isotropen Antenne wächst mit der Wellenlänge:

(2) A_W = λ²/(4 π)

Bei einer Strahlungsdichte S empfängt sie die Leistung P_r:

(3) P_r = S * A_W

Setzt man (1) und (2) in (3) ein, folgt:

(4) P_r = P / (4 π R²) * λ²/(4 π) = P * (λ/(4 π R))²

Die Abhängigkeit der Empfangsenergie von der Entfernung und der Wellenlänge kann als eine Dämpfung aufgefasst werden, die Freiraumdämpfung.

Berechnung

Die Freiraumdämpfung ist das Verhältnis der ausgestrahlten Leistung P zur Leistung P_r, die eine isotrope Antenne am Ort R empfängt:

(5) F = P / P_r

Aus (4) und (5) ergibt sich für die Freiraumdämpfung F:

$F = \left( \frac{ 4 \cdot \pi \cdot R }{ \lambda } \right) ^2$

Häufig wird die Freiraumdämpfung dann als Funktion der Frequenz beziehungsweise der Wellenlänge angegeben. Ist f die Frequenz, c die Lichtgeschwindigkeit und λ die Wellenlänge, dann beträgt die frequenzabhängige Freiraumdämpfung F:

$F = \left( \frac{ 4 \cdot \pi \cdot R \cdot f }{ c } \right)^2$

Außer der Freiraumdämpfung treten in der Erdatmosphäre bei hohen Frequenzen durch molekulare Absorption (abhängig von den Resonanzfrequenzen des Wasserdampfs, Sauerstoffs und anderer Gase) sowie abhängig vom Luftdruck und insbesondere der Luftfeuchtigkeit zusätzliche Dämpfungen auf. Die reale Dämpfung nimmt sehr viel größere Werte an. Die Freiraumdämpfung ist die Dämpfung, die auch unter Idealbedingungen nicht unterschritten werden kann.

Beispiele

Beispiele:

• f=2,4 GHz, R=1000 km. Dann ist F = 10¹⁶ bzw. F = 160dB ^[1]
• f=2,4 GHz, R=30'000 km. Dann ist F = 10¹⁹ bzw. F = 190dB ^[2]
• f=10 GHz, R=30'000 km. Dann ist F = 10²⁰ bzw. F = 200dB ^[3]

Literatur

• Jürgen Detlefsen, Uwe Siart: Grundlagen der Hochfrequenztechnik. 2. Auflage, Oldenbourg Verlag, München Wien, 2006, ISBN 3-486-57866-9
• Hans Lobensommer: Handbuch der modernen Funktechnik. 1. Auflage, Franzis Verlag GmbH, Poing, 1995, ISBN 3-7723-4262-0

Referenzen

1. ↑ Google Rechner
2. ↑ Google Rechner
3. ↑ Google Rechner

Siehe auch

Pfadverlust