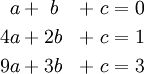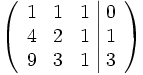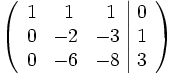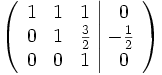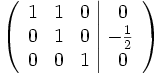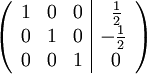Gauß-Jordan-Verfahren

Der Gauß-Jordan-Algorithmus ist ein Algorithmus aus den mathematischen Teilgebieten der linearen Algebra und Numerik. Mit dem nach Carl Friedrich Gauß und Wilhelm Jordan benannten Verfahren lässt sich die Lösung eines linearen Gleichungssystems berechnen. Es ist eine Erweiterung des gaußschen Eliminationsverfahrens, bei dem in einem zusätzlichen Schritt das Gleichungssystem bzw. dessen erweiterte Koeffizientenmatrix auf die reduzierte Stufenform gebracht wird. Daraus lässt sich dann die Lösung direkt ablesen.

Umformungsschritte

1. Man wählt die erste Spalte von links, in der mindestens ein von Null verschiedener Wert steht.
2. Ist die oberste Zahl der gewählten Spalte eine Null, so vertauscht man die erste Zeile mit einer anderen Zeile, in der in dieser Spalte keine Null steht.
3. Man dividiert die erste Zeile durch das nun oberste Element der gewählten Spalte.
4. Man subtrahiere von den übrigen Zeilen entsprechende Vielfache der ersten Zeile mit dem Ziel, dass das erste Element jeder Zeile (außer der ersten) Null wird.
5. Durch Streichen der ersten Zeile und Spalte erhält man eine Restmatrix auf die man diese Verfahren wieder anwendet. Das führt man solange durch, bis die Matrix in Zeilenstufenform ist.
6. Man zieht danach von den darüberliegenden Zeilen entsprechende Vielfache ab, sodass über einer führenden 1 nur Nullen stehen.

Beispiel

Es ist das folgende lineare Gleichungssystem gegeben:

$\begin{align} a &+ \ b&+ \ c = 0\\ 4a &+ 2b&+ \ c = 1\\ 9a &+ 3b&+ \ c = 3 \end{align}$

Es wird nun die erweiterte Koeffizientenmatrix des Gleichungssystems gebildet. In der ersten Spalte stehen die Faktoren der Variable a, in der zweiten die der Variable b, in der dritten die der Variable c und in der vierten die rechte Seite des Gleichungssystems. Ziel ist es nun, dass auf der linken Seite die Einheitsmatrix steht.:

$\left(\begin{array}{ccc|c} 1 & 1 & 1 & 0 \\ 4 & 2 & 1 & 1 \\ 9 & 3 & 1 & 3 \end{array}\right)$

Es werden nun folgende Zeilentransformationen vorgenommen:

• Zu Zeile 2 wird addiert: -4 * Zeile 1.
• Zu Zeile 3 wird addiert: -9 * Zeile 1.

Damit ergibt sich:

$\left(\begin{array}{ccc|c} 1 &\ 1 &\ 1 & 0 \\ 0 & -2 & -3 & 1 \\ 0 & -6 & -8 & 3 \end{array}\right)$

• Zu Zeile 3 wird addiert: -3 * Zeile 2.
• Zeile 2 wird dividiert durch -2.

$\left(\begin{array}{ccc|c} 1 & 1 & 1 &\ 0 \\ 0 & 1 & {3 \over 2} & -{1 \over 2} \\ 0 & 0 & 1 &\ 0 \end{array}\right)$

• Zu Zeile 1 wird addiert: -1 * Zeile 3.
• Zu Zeile 2 wird addiert: -3/2 * Zeile 3.

$\left(\begin{array}{ccc|c} 1 & 1 & 0 &\ 0 \\ 0 & 1 & 0 &-{1 \over 2} \\ 0 & 0 & 1 &\ 0 \end{array}\right)$

• Zu Zeile 1 wird addiert: -1 * Zeile 2.

$\left(\begin{array}{ccc|c} 1 & 0 & 0 &\ {1 \over 2} \\ 0 & 1 & 0 & -{1 \over 2} \\ 0 & 0 & 1 &\ 0 \end{array}\right)$

Diese Matrix wird auf unsere Gleichungen zurück übertragen. Wir erhalten:

$a = \frac{1}{2} \; ; \ b = -\frac{1}{2} \; ; \ c = 0$ .

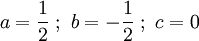Literatur

• Howard Anton: Lineare Algebra. Spektrum Akademischer Verlag GmbH Heidelberg, Berlin, ISBN 3-8274-0324-3

Weblinks

• Applet zum Lösen linearer Gleichungssysteme
• Das Gauß-Jordan-Verfahren interaktiv mit vollständigen Lösungswegen