Gebundene Variable

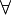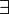Eine Variable bezeichnet man als frei in einer Formel der Prädikatenlogik, wenn sie in der Formel an wenigstens einer Stelle unquantifiziert (also nicht im Bereich eines Quantors zu dieser Variable) vorkommt. Eine mit einem Quantor ($\forall$ oder $\exists$) verwendete Variable heißt gebunden. Eine Formel ohne freie Variablen wird geschlossene Formel, Aussage oder Satz genannt.

Ein und dieselbe Variable kann in einer Formel sowohl freie als auch gebundene Vorkommen haben. Die Kenntnis von freien und gebundenen Variablen wird für die Bereinigung von Formeln benötigt.

Freie und gebundene Variablen kommen auch in anderen mathematischen Gebieten vor, z. B. im Lambda-Kalkül. Außerdem enthalten viele mathematische Notationen gebundene Variablen, etwa als Integrationsvariable oder Summationsvariable.

Beispiele

• In der (geschlossenen) Formel 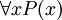$\forall x P(x)$ kommt x nicht frei, aber gebunden vor.
• In der Formel 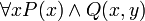$\forall x P(x) \and Q(x,y)$ ist das Vorkommen von x in P(x) gebunden, das Vorkommen in Q(x,y) und die Variable y sind frei (man beachte, dass sich der Allquantor nur auf die Teilformel P(x) erstreckt).
• In der Formel 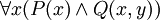$\forall x ( P(x) \and Q(x,y))$ ist x gebunden und y ist frei.

Weitere Begriffe

• Gebundene Umbenennung: Eine durch einen Quantor gebundene Variable kann durch eine andere (vorher nicht vorkommende) ersetzt werden, wobei eine logisch äquivalente Formel entsteht. Beispiel: Aus 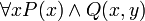$\forall x P(x) \and Q(x,y)$ entsteht durch gebundene Umbenennung die Formel $\forall z P(z) \and Q(x,y)$.
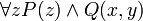• Vollfreie Variable: Eine freie Variable ohne gebundenes Vorkommen nennt man auch vollfrei. Durch gebundene Umbenennung kann man jede Formel in eine logisch äquivalente umformen, in der alle freien Variablen tatsächlich vollfrei sind.

Mathematische Notationen mit gebundenen Variablen

In den folgenden mathematischen Notationen (und vielen weiteren) wird eine gebundene Variable verwendet:

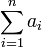
$\sum_{i=1}^{n}a_i$	(Summe endlich vieler Werte)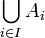
$\bigcup_{i \in I} A_i$	(Vereinigung einer Familie von Mengen)
$\int_a^b f(x)\,\mathrm dx$	(Bestimmtes Integral)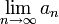
$\lim_{n\to\infty} a_n$	(Grenzwert einer unendlichen Folge)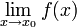
$\lim_{x \to x_0} f(x)$	(Grenzwert einer Funktion an der Stelle x0)

Literatur

H.-P. Tuschik, H. Wolter: Mathematische Logik – kurzgefaßt. Spektrum, Akad. Verl., Heidelberg 2002, ISBN 3-8274-1387-7.